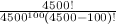How to stitch two meshes together along overlapping seams without altering other parts of the meshes?

Question

I'm trying to join two meshes together into one single mesh. The boundary edges of both overlap perfectly, but they do not have the same spacing - thus, all faces touching the seams need to be deleted and then all the points from those faces (including those along the seam) need to be re-triangulated to close the gap.

See an example of the two meshes:

The blue area here is very fine mesh Here the seam is exaggerated

There is a coarse mesh and a dense mesh as you can see from the first image. I need to stitch these two together along the seams.

The problem is that the seams can be very random and hard to generalize.

I also have the condition that I can't do a constrained delaunay and re-triangulate everything because there are parts of my mesh where z != F(x,y) , and this gets messed up by the delaunay. I can only modify the faces touching the seams.

Preferably a vtk based solution if anyone can help?

I've tried vtk.vtkDelaunay2D to re-mesh.

I also tried vtk.vtkFeatureEdges to extract the edges. Then tried to split the boundary points into segments, find which segments overlapping with the other mesh segments and using Delaunay on sets of segments something like this:

which didnt work since the seams are overlapping perfectly I think?

I got vtk.vtkDecimatePro to work fine but I don't want to actually modify the mesh. I only want to stitch the seams.

If anyone has any ideas, I'm running out.

Answer 1

It's hard to say what will work for your real use case, but I cobbled together something using two mismatched cylinders as example data.

The idea is pretty much what you laid out, just perhaps done a bit more carefully:

1. find the boundary edges of both meshes
2. use some heuristic to identify edges that should be fused (I assume this is already solved for your use case),
3. pull out cells in both meshes that contain the respective edge lines, delete these cells (along with edge points) from the original meshes
4. triangulate these cells using delaunay_3d()
5. use some heuristic to discard the "capping" introduced by triangulation; looking at your screenshot what I did will probably work: check the cell normals and discard "too horizontal" cells
6. merge the two truncated input meshes and the middle triangulated strip

I've left some comments in the code, e.g. the assumption that your meshes are triangulated, or if not they can be triangulated. If we can't triangulate the meshes then remove_points() won't work, so we'd have to mess around with cell extraction to get the same result (not too difficult, just more fiddly).

The code first plots the input meshes to show the mismatch, and it plots the merged mesh at the end. delaunay_3d() complains about mesh quality, which is probably related to the 8 larger triangles along the seam in the triangulation. Whether this is something that affects your real use case is not something I can guess.

import pyvista as pv

# plotting setup
theme = pv.themes.DocumentTheme()
theme.show_edges = True

# create dummy meshes
mesh1 = pv.Cylinder(resolution=8, center=(0, 0, 0.5), direction=(0, 0, 1), capping=False).triangulate().subdivide(3)
mesh2 = pv.Cylinder(resolution=16, center=(0, 0, -0.5), direction=(0, 0, 1), capping=False).triangulate().subdivide(3)
mesh2.rotate_z(360/32, inplace=True)

# plot them together
plotter = pv.Plotter(theme=theme)
plotter.add_mesh(mesh1, color='pink')
plotter.add_mesh(mesh2, color='cyan')
plotter.show()

edge_kwargs = dict(
    manifold_edges=False,
    non_manifold_edges=False,
    feature_edges=False,
    boundary_edges=True,
)

def tag_and_extract(mesh):
    """The work we have to do for both meshes.

    This adds some scalars and extracts cells involved in the common
    edge of both meshes. You'll need to tweak the filtering that selects
    the appropriate feature edges below, see the "first hack" comment.

    This will also modify the input mesh by deleting edge points and
    the cells containing them. If you want to preserve your input
    mesh, pass in a copy, and use that copy after calling this
    function.

    """
    # grab interesting edges
    # add scalars to keep track of point and cell indices after extraction
    mesh.point_data['point_inds'] = range(mesh.n_points)
    mesh.cell_data['cell_inds'] = range(mesh.n_cells)
    mesh_edges = mesh.extract_feature_edges(**edge_kwargs)

    # first hack:
    # you'll need some way to locate corresponding pairs of edges; this is specific to your problem
    # in this example there's only one pair of edges so we'll clip with two planes
    mesh_edges = mesh_edges.clip('z', origin=mesh1.center).clip('-z', origin=mesh2.center)

    # extract original cells containing edge lines
    mesh_edge_cells = mesh.extract_points(mesh_edges['point_inds'])

    # delete edge points along with their containing cells
    # the example data is already triangulated, otherwise we'd have to triangulate it
    # (or have to do more work)
    mesh.remove_points(mesh_edges['point_inds'], inplace=True)

    return mesh_edge_cells

mesh1_edge_cells = tag_and_extract(mesh1)
mesh2_edge_cells = tag_and_extract(mesh2)

# triangulate the edge strip
edge_strip = (mesh1_edge_cells + mesh2_edge_cells).delaunay_3d().extract_surface()

# second hack that needs fitting to your problem: remove capping
normals = edge_strip.compute_normals().cell_data['Normals']
horizontals = abs(normals[:, -1]) < 0.9  # has lots of leeway
edge_strip = edge_strip.extract_cells(horizontals).extract_surface()

# merge meshes
merged = mesh1 + edge_strip + mesh2

# plot the result
plotter = pv.Plotter(theme=theme)
plotter.add_mesh(merged)
plotter.show()

Screenshot of the input meshes:

Merged mesh:

Hopefully there are better (and more reliable) ways to do this, but this is my best guess.

Answer 2

I ended up modifying my approach, but hopefully it helps someone.

The original goal here was to take a high resolution mesh, and pass over it with a predefined grid size - if cells in a given grid square pass a certain test, then the grid square is kept instead of the original cells. This way, after checking all the squares, a portion of the mesh can have a drastically reduced resolution.

Whole goal here was to only reduce resolution in certain custom defined areas (not static areas either, but rule based).

Most of the solution is not pertinent to this question so I will just describe:

-group cells based on which grid squares their centroids land in

-decide which grid squares to keep (and thus which original cells to downsample)

-group together all the cells you want to downsample, and all the cells you want to keep (split the mesh into two parts)

-use vtk.vtkDecimatePro on on the part you want to downsample, and make sure you turn off boundary vertex deletion

-after downsampling, both meshes still have the same boundary so simply concatenate the meshes back together

The relevant bits of code are:

import vtk

def decimate_polydata(polydata, 
                      reduction=0.5, 
                      error=0.01, 
                      accumulate_error=False,
                      degree=25,
                      feature=15,
                      splitting=True):
    '''
    Function to decimate a VTK polydata object
    '''
    deci = vtk.vtkDecimatePro()
    deci.SetTargetReduction(reduction)
    deci.PreserveTopologyOn()
    deci.SetFeatureAngle(feature)
    deci.SetSplitting(splitting)
    deci.SetErrorIsAbsolute(1)
    deci.SetAccumulateError(accumulate_error)
    deci.SetMaximumError(error)
    deci.SetDegree(degree)
    deci.BoundaryVertexDeletionOff() #this is the key!!
    deci.SetInputData(polydata)
    deci.Update()
    deci = deci.GetOutput()
    return deci

def merge_polydata(polydatas):
    '''
    Function to append/merge two VTK polydata objects together
    pt and cell indexing is updated automatically
    '''
    poly = vtk.vtkAppendPolyData()
    for polydata in polydatas:
        poly.AddInputData(polydata)
    poly.Update()
    poly = poly.GetOutput()
    return poly

The result is similar to what I had previously, but instead of there being squares in the coarse areas, it's just decimated: