I stuck with creating a sparse matrix, in which I can count cross-selling frequency of products based on the cart and product ids.
Sample data frame:
x = data.frame(
cart_id = c("1","1","1","2","2","3","4","5","5","6"),
product_id = c("A","B","C","D","A","F","G","A","C","F")
)
The most desirable output: a sparse matrix with the number of times that two of products appeared in the same cart.
Any hints?
EDIT:
Both answers solve the problem.
This is a very interesting problem/application!!!
Your two-column data.frame x shows what product is in what cart, but you are interested in an event that products i and j fall into the same cart. You don't care what particular cart it is; instead, you want to count how many times such an event happens.
Certainly, your expected output is a contingency table (a square matrix with counts). However, the counts must be first computed, which is not a trivial task. The following well-commented function does this.
Contingency <- function (product_id, cart_id) {
## unique product ID
ProductID <- unique(product_id)
## let's use a consecutive numeric ID for product
ProductIDnum <- match(product_id, ProductID)
## split products by cart
CartItems <- unname(split(ProductIDnum, cart_id))
## number of products in each cart
nItemsPerCart <- lengths(CartItems)
## we are only interested in carts with 2+ different products
CartItems <- CartItems[nItemsPerCart >= 2]
CartItems <- lapply(CartItems, sort)
## an event: a pair of products (i, j) fall into one same cart
## (note that we don't care which particular cart it is)
## here, `Events` is a 2-column matrix where each row is an event
## this matrix will have duplicated rows so that we can `aggregate`
Events <- t(do.call("cbind", lapply(CartItems, combn, m = 2)))
## aggregate: how many times does each event happen?
Freq <- aggregate(rep(1, nrow(Events)), data.frame(Events), sum)
## (i, j, x) triplet for a "TsparseMatrix"
i <- Freq[[1]]
j <- Freq[[2]]
x <- Freq[[3]]
## the dimension of the square matrix
n <- length(ProductID)
Matrix::sparseMatrix(i = i, j = j, x = x, symmetric = TRUE, dims = c(n, n),
dimnames = list(ProductID, ProductID))
}
Now we can apply it to your dataset x.
mat <- Contingency(x$product_id, x$cart_id)
#6 x 6 sparse Matrix of class "dsCMatrix"
# A B C D F G
#A . 1 2 1 . .
#B 1 . 1 . . .
#C 2 1 . . . .
#D 1 . . . . .
#F . . . . . .
#G . . . . . .
## dense form (not recommended if there are lots of products)
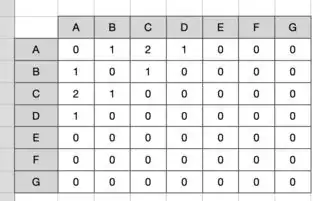
as.matrix(mat)
# A B C D F G
#A 0 1 2 1 0 0
#B 1 0 1 0 0 0
#C 2 1 0 0 0 0
#D 1 0 0 0 0 0
#F 0 0 0 0 0 0
#G 0 0 0 0 0 0
You may also use xtabs and crossprod:
mat <- Matrix::crossprod(xtabs(~ ., data = x, sparse = TRUE))
#6 x 6 sparse Matrix of class "dsCMatrix"
# A B C D F G
#A 3 1 2 1 . .
#B 1 1 1 . . .
#C 2 1 2 . . .
#D 1 . . 1 . .
#F . . . . 2 .
#G . . . . . 1
The only thing left is to set diagonal entries to zeros:
diag(mat) <- 0
mat
# A B C D F G
#A 0 1 2 1 . .
#B 1 0 1 . . .
#C 2 1 0 . . .
#D 1 . . 0 . .
#F . . . . 0 .
#G . . . . . 0
But note that "diag<-" is not doing a very neat job here, as the replacement 0 is not treated as zero, in the storage sense.
Damm!!! I just found a dupe for this: Creating co-occurrence matrix.
A base R option using as.dist + ´crossprod+table` can make it
> as.matrix(as.dist(crossprod(table(x))))
A B C D F G
A 0 1 2 1 0 0
B 1 0 1 0 0 0
C 2 1 0 0 0 0
D 1 0 0 0 0 0
F 0 0 0 0 0 0
G 0 0 0 0 0 0
