Animated flight path plot in python

Question

I would like to write a program for plotting an animated 3D ribbon image in python. The ribbon follows the flight path as provided by a log containing the following information:

Timestamp, pitch, roll, altitude, latitude, longitude, heading, turn rate.

The final figure should look something like this (without the aircraft figure).

Aircraft manoeuvres:

Please let me know how this can be done.

Edit: Heading is the angle between the flight and the north direction. It is a scalar quantity measured in degrees.

Turn rate is rate of change of heading.

Pitch is up/down rotation and roll is rotation given by rolling over on either side. They are measured in degrees.

Below is a sample of the data:

Time: 801.475 alt (ft): 12599.88668 lat(deg): 63.94230675 lon(deg): -22.72656178 pitch(deg): 39.60080719 roll(deg): 40.49394608 heading(deg): 344.7094606 turnspeed: 8.104816363

These are all from the inertial frame of reference, which can also serve as axes for this plot.

Thank you

Answer 1

This is not a complete answer.

First, you need to convert your data to x,y,z coordinates. let's say that you use feet, then you have to convert latitude and longitude to x,y. It will not work if the plane moved a long distance, because the earth is not flat.

Your pitch, roll and heading data serves to calculate the (x,y,z) coordinates of the tips of the wings (or the border of the ribbon) relative to the (x,y,z) of the center of the plane. You need quaternions or geometric algebra to do that. You can also do it with basic trigonometry, but you risk gimbal lock bugs.

Then you need to interpolate your data, for the timestep you choose.

With your interpolated data, you get 2 arrays of (x,y,z) for each ribbon border, which you can plot as lines in 3D. To do the plot you need to choose a position of the viewer, and a direction to which he is looking at.

If you want to do an animation, you use the same data, but google how to do animations after you managed to do the interpolations.

When the position of the plane at the time t, t+1 is

position[t]  =[x,y,z]
position[t+1]=[x1,y1,z1]

the direction at which the plane is moving is

velocity[t+1/2]=position[t+1]-position[t]=[x1-x,y1-y,z1-z]/(t+1/2-t)

From the Position[t], you have to calculate the position of the right wing tip WR[t], and left wing tip WL[t], which are the [x,y,z] coordinates of the ribbons at the time t

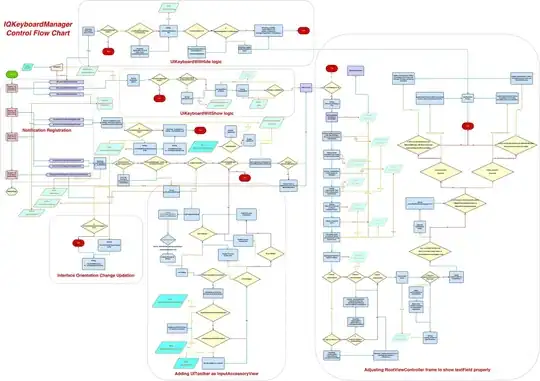
Now, following this convention from Wikipedia

If we conjecture that the viewer is looking at the North, X is positive towards East, Y is positive towards the North, and Z is positive away from the center of earth (That depends on how did you converted latitude/longitude to x,y)

-If the length of a wing is L, then the coordinate of the rigth wing tip, relative to the center of the plane Position[t], would be [L,0,0], when the plane is leveled, aiming at the North.

At the time t the right wing tip WR[t] shold be at coordinates:

WR[t] = Position[t] + RotateVectorByRoll(RotateVectorByPitch(RotateVectorByHeading([L,0,0], Θh), ΘP), ΘR)