Can I define my own vectors to run an interaction model using deseq2?

Question

just wondering whether someone could help me evaluate my bulk-RNA seq design, please? I am looking at liver transplant samples taken before and after undergoing machine perfusion but some of them have an additional leukocyte filter in place. I've defined my own vectors for each condition (rather than using the defined outputs from resultsNames(dds) and set up an interaction model.

I've come up with three models and struggling to pick the one that accurately answers my question.

Question: How does the addition of a leukocyte filter to the rig (machine perfusion) change differential expression when compared to machine perfusion alone?

colData: meta

Design 1: (my favorite)

dds = DESeqDataSetFromMatrix(countData = counts,
                             colData = colData,
                             design = ~ batch + filter + perfusion + filter:perfusion)

#get model matrix
mod_mat <- model.matrix(design(dds), colData(dds))

#define vectors for each condition

filter_yes <- colMeans(mod_mat[dds$filter == "yes", ])
filter_no <- colMeans(mod_mat[dds$filter == "no", ])

res <- results(dds, contrast = filter_yes - filter_no)

Design 2:

dds = DESeqDataSetFromMatrix(countData = counts,
                             colData = colData,
                             design = ~ batch + sex + test)

res <- results(dds, contrast = c("test", "post yes","post no" ))

Design 3:

dds = DESeqDataSetFromMatrix(countData = counts,
                             colData = colData,
                             design = ~ batch + filter + perfusion + filter:perfusion)

res <- results(dds, contrast = list(c("filteryes.perfusionpost")))

I can appreciate that designs 1 and 3 use an interaction model. But I feel like design 1 most accurately answers my question as I define vectors myself and only look at the differences in the addition of a filter group but still including perfusion.

Thanks for reading,
Q

Answer 1

I don't know enough about the biology here to know what approach is the "correct". But, I'll try to clarify some of the meaning of the contrasts you have and give my opinion at the end.

Firstly a note on terminology: what you refer to as "design 1" and "design 3" are actually the same design (the formula is the same in both). The difference is the contrast that you are considering in each case.

I'll discuss those two cases, and not cover the design with the sex variable (by ignoring sex you are effectively absorbing sex-related variation in expression into the residual error of the model).

I'll create a fake dataset with the same variables you have, in case readers want to recreate these contrasts (for future reference, responders really appreciate it if you do something like this when posting questions on stackoverflow - see this post for more details, and this one specifically discussing R).

library(DESeq2)

# example data - ignoring sex
dds <- makeExampleDESeqDataSet(m = 32)
dds$perfusion = c(rep(c("pre", "post"), each = 10), rep(c("pre", "post"), each = 6))
dds$filter = c(rep(c("no", "yes", "no", "yes"), each = 5), rep(c("no", "yes", "no", "yes"), each = 3))
dds$batch = c(rep("data1", 20), rep("data2", 12))

dds$perfusion <- factor(dds$perfusion, levels = c("pre", "post"))
dds$filter <- factor(dds$filter)
dds$batch <- factor(dds$batch)

# define design and fit the model
design(dds) <- ~ batch + filter + perfusion + filter:perfusion
dds <- DESeq(dds)

Let's make an illustrative diagram showing examples of what this model represents:

In this example, we can see that:

• batch has an average effect that is equal across all the groups, on average expression is higher in batch 2.
• filter has a positive effect (lines slope upwards)
• perfusion also has a positive effect (orange lines are above green lines)
• there is an interaction, i.e. the response to having a filter is different depending on whether it's pre- or post-perfusion (the slopes of the orange and green lines are different).

Contrast 1 - mean difference between filter

In your first case, you were defining contrasts using a numeric vector, as illustrated in this tutorial:

# get model matrix
mod_mat <- model.matrix(design(dds), colData(dds))

# define vectors for each condition
filter_yes <- colMeans(mod_mat[dds$filter == "yes", ])
filter_no <- colMeans(mod_mat[dds$filter == "no", ])

# get the results 
res <- results(dds, contrast = filter_yes - filter_no)

In this case, what you are comparing is the average effect of filter, across both levels of perfusion (and batch). This can be illustrated in this diagram:

Is this OK? It might be fine, but consider this (somewhat extreme) example:

Now, there is no difference in the average effect of filter, but clearly filter has an effect, it's just reversed between pre- and post-perfusion. (maybe this doesn't make sense in your case, again I'm not familiar with the biological details to be able to comment on that).

Contrast 2 - interaction term

In your third example, you were testing for the interaction between the two predictors in your design. This is illustrated here:

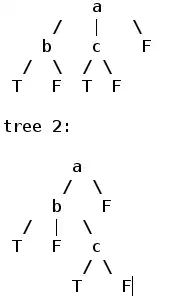
Notice that the effects are still being averaged across both batches, but now we are considering all 4 combinations of the levels of the other two factors.

How to define contrasts using numeric vectors?

You correctly defined the contrast for the interaction term using DESeq's default coefficient names. If you wanted to define it using numeric vectors, this is how you would have to do it:

# define vectors for each condition - need to consider both predictors!
filter_yes_perfusion_pre <- colMeans(mod_mat[dds$filter == "yes" & dds$perfusion == "pre", ])
filter_yes_perfusion_post <- colMeans(mod_mat[dds$filter == "yes" & dds$perfusion == "post", ])
filter_no_perfusion_pre <- colMeans(mod_mat[dds$filter == "no" & dds$perfusion == "pre", ])
filter_no_perfusion_post <- colMeans(mod_mat[dds$filter == "no" & dds$perfusion == "post", ])

And all the possible tests (including the interaction):

# filter difference for pre
res <- results(dds, contrast = filter_yes_perfusion_pre - filter_no_perfusion_pre)

# filter difference for post
res <- results(dds, contrast = filter_yes_perfusion_post - filter_no_perfusion_post)

# perfusion difference for yes
res <- results(dds, contrast = filter_yes_perfusion_post - filter_yes_perfusion_pre)

# perfusion difference for no
res <- results(dds, contrast = filter_no_perfusion_post - filter_no_perfusion_pre)

# interaction (difference of differences)
res1 <- results(dds, contrast = (filter_yes_perfusion_post - filter_yes_perfusion_pre) - (filter_no_perfusion_post - filter_no_perfusion_pre))

Incidentally, your first contrast can also be defined from these, it would be equivalent to setting the contrast as:

(filter_yes_perfusion_post + filter_yes_perfusion_pre)/2 - (filter_no_perfusion_post + filter_no_perfusion_pre)/2

I.e. the average of "yes" minus the average of "no".

Which contrast is "correct"?

I don't think there's a right answer for this - it does depend on your question and what makes sense in your system of study. You phrased your question as:

How does the addition of a leukocyte filter to the rig (machine perfusion) change differential expression when compared to machine perfusion alone?

If I'm understanding the system correctly, it only makes sense to ask for the effect of the filter after (or post) perfusion, since before perfusion nothing should be different. However, you rightly want to account for differences before (pre) perfusion. If that's the case, then you should be testing for the interaction (contrast 2 above). In other words, you want to know what is the difference of having a filter post-perfusion compared to any differences that existed pre-perfusion.