Is the following statement equivalent?
foldr (++) [ ] = foldl (++) [ ]
I know that foldr (+) 0 = fold (+) 0 is equivalent and for the operator (-) it's not, but how about the (++) operator ?
I think the result is a list with the same content but in another order. Is the order of the list relevant?
EDIT: does not answer the question (sorry)
foldl :: (b -> a -> b) -> b -> [a] -> b
foldr :: (a -> b -> b) -> b -> [a] -> b
(+) is commutative, i.e. produces the same result if the arguments order is switched. E.g. 1+2 is the same as 2+1.
Look at the type signature of foldl and foldr.
foldl takes a function (b->a->b) whose second argument is an element from the list.
On the other hand, foldr takes a function (a->b->b) whose first argument is an element from the list.
With foldl, there is an accumulation on the left (first argument). With foldr, there is an accumulation on the right (second argument).
foldl folds from left to right, foldr folds from right to left.
Technically, it's more complicated than that. For more information, see https://wiki.haskell.org/Foldr_Foldl_Foldl'
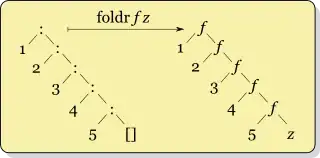
Both expressions return the in order concatenation of all sublists in the rightmost argument, so they are functionally identical, at least for finite sublists.
Let's check using the Haskell ghci interpreter:
$ ghci
GHCi, version 8.10.5: https://www.haskell.org/ghc/ :? for help
...
λ>
λ> xss = [[1,2], [3,4,5], [6,7,8,9]]
λ>
λ> foldr (++) [] xss == foldl (++) [] xss
True
λ>
λ> foldr (++) [] [[1,2], [3,4,5], [6,7,8,9]]
[1,2,3,4,5,6,7,8,9]
λ>
λ> foldl (++) [] [[1,2], [3,4,5], [6,7,8,9]]
[1,2,3,4,5,6,7,8,9]
λ>
But that's not the whole story. For example, any programmer who has been thru the usual lectures about sorting algorithms knows that bubble sort and QuickSort are functionally equivalent. Both algorithms return the ordered version of the input array.
But QuickSort is practical, and bubble sort is useless except for small input arrays.
It is a bit similar here.
Let's turn statistics on in our ghci interpreter:
λ>
λ> :set +s
λ>
λ> length $ foldl (++) [] (replicate 5000 [1,2,3,4])
20000
(3.31 secs, 4,124,759,752 bytes)
λ>
λ> length $ foldl (++) [] (replicate 10000 [1,2,3,4])
40000
(16.94 secs, 17,172,001,352 bytes)
λ>
So if we double the number of input sublists, the volume of memory allocations is multiplied by 4, not 2. The algorithm is quadratic here, hence horribly slow, like bubble sort.
And no, replacing foldl by its strict sibling foldl' will not help. The root of the problem is that operator (++) has to duplicate its left operand, because it is not feasible in Haskell to just alter its last pointer to next node, like you would do in C/C++. However, operator (++) can just use a simple pointer to its right operand, because the right operand is immutable, as is any Haskell named value.
In summary, for the left operand, immutability works against us. For the right operand, it works for us.
In the case of foldl, the left operand is the accumulator. So we repeatedly have to duplicate our (large and growing) accumulator. This is what breaks the performance symmetry between foldl and foldr.
We can readily check that the performance of foldr is much better:
λ>
λ> length $ foldr (++) [] (replicate 5000 [1,2,3,4])
20000
(0.02 secs, 1,622,304 bytes)
λ>
λ> length $ foldr (++) [] (replicate 10000 [1,2,3,4])
40000
(0.02 secs, 3,182,304 bytes)
λ>
because here dynamic memory allocation is multiplied by 2, not 4.
I don't know how useful this is for you, but I wanted to use this as an excuse for learning Agda. So here's a formal proof:
Imports
import Relation.Binary.PropositionalEquality as Eq
open Eq using (_≡_; refl; cong; sym)
open Eq.≡-Reasoning using (begin_; _≡⟨⟩_; step-≡; _∎)
Definitions
data List (A : Set) : Set where
[] : List A
_::_ : (x : A) (xs : List A) -> List A
variable
A : Set
B : Set
foldr : (A -> B -> B) -> B -> List A -> B
foldr k z [] = z
foldr k z (x :: xs) = k x (foldr k z xs)
foldl : (B -> A -> B) -> B -> List A -> B
foldl k z [] = z
foldl k z (x :: xs) = foldl k (k z x) xs
_++_ : List A -> List A -> List A
[] ++ ys = ys
(x :: xs) ++ ys = x :: (xs ++ ys)
Theorems
++-assoc : ∀ (xs ys zs : List A)
-> xs ++ (ys ++ zs) ≡ (xs ++ ys) ++ zs
++-assoc [] ys zs = refl
++-assoc (x :: xs) ys zs = cong (x ::_) (++-assoc xs ys zs)
++-[] : ∀ (xs : List A)
-> xs ++ [] ≡ xs
++-[] [] = refl
++-[] (x :: xs) = cong (x ::_) (++-[] xs)
helper : ∀ (x : List A) (ys : List (List A))
-> x ++ foldl _++_ [] ys ≡ foldl _++_ x ys
helper x [] = ++-[] x
helper x (y :: ys) =
begin
x ++ foldl _++_ [] (y :: ys)
≡⟨⟩
x ++ foldl _++_ y ys
≡⟨ cong (x ++_) (sym (helper y ys)) ⟩
x ++ (y ++ foldl _++_ [] ys)
≡⟨ ++-assoc x y (foldl _++_ [] ys) ⟩
(x ++ y) ++ foldl _++_ [] ys
≡⟨ helper (x ++ y) ys ⟩
foldl _++_ (x ++ y) ys
≡⟨⟩
foldl _++_ x (y :: ys)
∎
proof : ∀ (xs : List (List A))
-> foldr _++_ [] xs ≡ foldl _++_ [] xs
proof [] = refl
proof (x :: xs) =
begin
foldr _++_ [] (x :: xs)
≡⟨⟩
x ++ foldr _++_ [] xs
≡⟨ cong (x ++_) (proof xs) ⟩
x ++ foldl _++_ [] xs
≡⟨ helper x xs ⟩
foldl _++_ x xs
≡⟨⟩
foldl _++_ [] (x :: xs)
∎
I hope that is kind of readable even if you only know Haskell.
This was more work than I expected. It's not obvious knowing only associativity of _++_.
Oh, and I'm sure it is not so hard to generalize this to any associative operation with an identity element. I'll leave that as an exercise to the reader.
And finally I should note that this only holds for finite lists.
