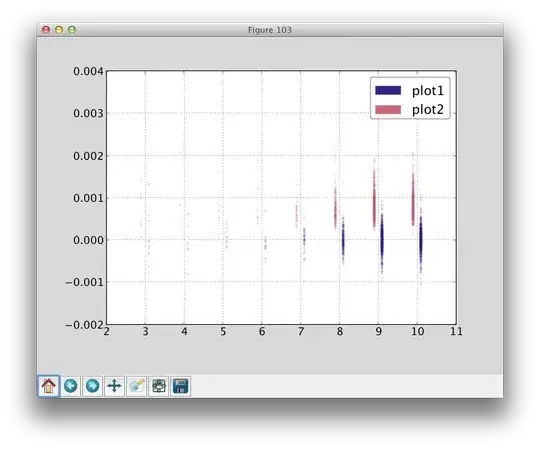
Problem: I have ring-like binary images with varying thicknesses. I want to calculate its thickness at n places of that ring-like segment.
My approach: Find the medial axis and distance transform. The distance transform maximizes at the medial axis, so I can use those distances and explain the thicknesses as distance*2.
Challenge: Since the images are a bit complex, when I use skimage.morphology.medial_axis to calculate the medial axis and distance transform, the medial axis branches at some points, which I do not want. I want a single ring-like medial axis without any branching. This messes up the distance transform results as well.
What I tried: I used NetworkX and refined the medial axis.
Now my questions: To answer my initial problem, how to calculate the distance from the medial axis to the 2 boundaries at equidistant n points on the medial axis?.
Also is there any better way of answering my initial question?
I am using Python 3.9
Thank you in advance.