C++ recursion. Why won't my recursion method call back to itself

Question

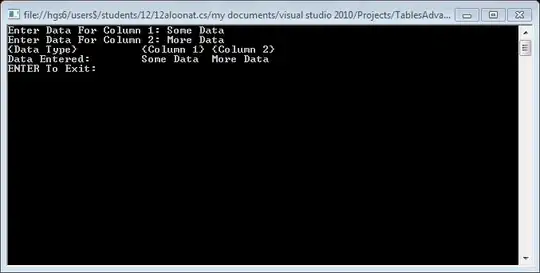
i am not sure how to resolve this math problem. what should i recall and where did i miss something. i have tried different opportunities. i think i just call not existing index or something like that..

#include <iostream>
using namespace std;
double recur(int n, int x);
double x;
int number;

int main()
{
    cout << "enter n: " ;
    cin >> number;
    cout << endl;
    do
    {
        cout << "enter float x!=0: ";
        cin >> x;
        cout << endl;
    } while (x==0);
    cout << "recur(" << number << "," << x << ")=" << recur(number, x) << endl;
    system("pause");
}
double recur(int n, int x)
{
    if (n > 1) return (x * recur(n, x - n) * recur(n - 1, x));
    else if( n == 1) return x * recur(n,x) - x;
    else return 1;
}

Formula:

Why are your variables global? I also don't see how you can ever reach your base case. Of the three recursive calls, only one ever decrements `n`, and notably the case of `n == 1` appears to recurse infinitely. And maybe it's just my simple mind, but it's not obvious what you're trying to do in your recursive function, and the name isn't helping at all. — sweenish, Oct 21 '22 at 19:35
Have you tried running your code line-by-line in a debugger while monitoring the values of all variables, in order to determine in which line your program stops behaving as intended? If you did not try this, then you may want to read this: [What is a debugger and how can it help me diagnose problems?](https://stackoverflow.com/q/25385173/12149471) You may also want to read this: [How to debug small programs?](https://ericlippert.com/2014/03/05/how-to-debug-small-programs/) — Andreas Wenzel, Oct 21 '22 at 19:39
You have a `double x` at global scope that will be supplanted by an `int x` in `recur`. Even if this is correct, it makes the code harder to read. — user4581301, Oct 21 '22 at 19:39
Your code would be easier to read (both for yourself and other people) if you used [indentation](https://en.wikipedia.org/wiki/Indentation_style). EDIT: Meanwhile, someone else has fixed it for you. — Andreas Wenzel, Oct 21 '22 at 19:40
Off-Topic: You should rename your function. There are many uses for recursion, especially math. For example, does `recur` calculate a Fibonacci number? Is is a Taylor Series expansion? One can't tell from the `recur` name; only speculate. — Thomas Matthews, Oct 21 '22 at 20:58
You don't even have a logarithm anywhere in your recursive function, so it has no chance of being correct. But your base case is n==1, which is the second line of the formula. if n>1 then use the first line of the formula — President James K. Polk, Oct 21 '22 at 23:51
When you attempt something new, it is wise to attempt it in the simplest way that you can imagine. When you write your first recursive function, choose a simple formula of integer arithmetic, not calculus. — Beta, Oct 22 '22 at 02:35
I think your recursion for the `n>1` case is slightly malformed: Your recursive function is for calculating the _integral_ of `F(x) dx` (where `F(x) = (ln x)^n` for brevity). However, that first term is `x * F(x)`, not `x * integral(F(x) dx)`. There should only be a single recursive call there, something like `x * pow(log(x), n) - recur(n - 1, x)`. — Rogue, Oct 27 '22 at 15:28
Fyi, `ln^n x` isn't the same as `(ln x)^n`, it's `ln(ln(... (x)))` where there are `n` calls to `ln` — Caleth, Oct 27 '22 at 16:20
@Caleth that seems to be the [formula](https://en.wikipedia.org/wiki/List_of_integrals_of_logarithmic_functions) for the integral of `(ln x)^n`, though. — Bob__, Oct 27 '22 at 16:56

score 0 · Answer 1 · answered Oct 27 '22 at 15:25

For formula:

It's implementation:

#include <iostream>
#include<cmath>
using namespace std;
double recur(int n, int x);
double x;
int number;

int main()
{
    cout << "enter n: " ;
    cin >> number;
    cout << endl;
    do
    {
        cout << "enter float x!=0: ";
        cin >> x;
        cout << endl;
    } while (x==0);
    cout << "recur(" << number << "," << x << ")=" << recur(number, x) << endl;
    system("pause");
}
double recur(int n, int x)
{
    if (n > 1) return (x*(pow(log(x),n)) - n*(recur(n-1,x)));
    else if( n == 1) return x * log(x) - x;
}

For n>1 line
(x*(pow(log(x),n)) = x*(ln x)^n
n*(recur(n-1,x)) = n* integral( (lnx)^(n-1) ) <- In next recursion call one power will get reduced

For n=1 line
x * log(x) - x = xlnx - x <- base condition(where recursive call will stop)

In this implementation recur(n,x) denotes integration of (lnx)^n w.r.t x.

score 0 · Answer 2 · answered Oct 27 '22 at 16:45

Your integral isn't the same as the log portion, so you should probably split that out.

double ln_n(int n, double x) {
    while (n --> 0) x = log(x);
    return x;
}

double integral(int n, double x) {
    if (n > 0) return (x * ln_n(n, x)) - (n * integral(n - 1, x));
    return x;
}

See it live

C++ recursion. Why won't my recursion method call back to itself

2 Answers2