Julia Stochastic Differential Equation Very Slow

Question

Please help me figure out why my code is sooo slow and possible ways to speed it up. I have used vectorization, @inbounds, column major indexing, @floop, and preallocation so I would think it would be faster. I am at a loss...

The code simulates a stochastic wave of cells (as in biological cells) and mutant cells. I am using the Euler-Murayama method to propagate the coupled (Chemical Langevin) equations:

Where W/M denotes the number of wild-type cells and mutant cells respectively, K is the carrying capacity (maximum number of cells), i denotes the deme (location), and N(0,1) is a normal random variable.

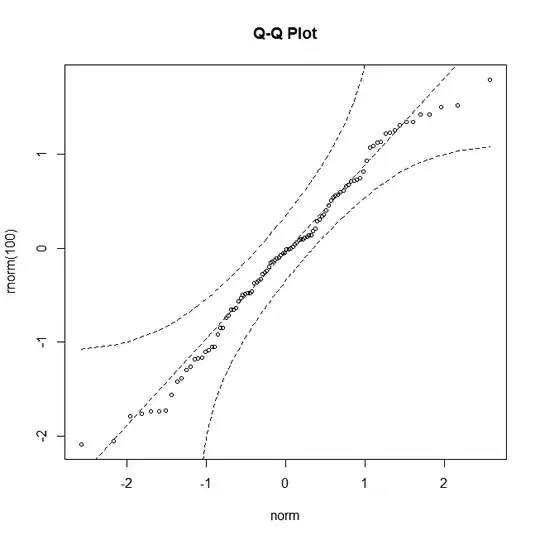
Here is a graphic of the waves after some time propagating:

I have attached the important part of the code below, and tried to comment it as best as I could.

using Random, Distributions
using StatsBase
using Statistics
using FLoops

# CLE Parameters/Set-Up:
K = 100 # Carrying capacity (maximum number of cells)
M = 100 # Number of demes (locations)
T = 100_000_000 # number of time steps
dt = 1e-1 # time increment
g = Normal(0.0,sqrt(dt)) # normal distribution with ave = 0.0, std_dev = dt
r_w = 0.1 # Wild-type growth rate
r_m = 0.2 # Mutant growth rate
r_wm = [r_w, r_m]' # Growth rate vector (transposed)
N = 1 # number of independent processes (slow even when N = 1)

# initial wave (essentially a step-function of wild-types 
# with 100 mutants at deme (location) 76)
state_init = Matrix(reshape(repeat([K, 0.0]',M+2),(M+2,2))) 
state_init[M÷2+2:end,1] .= 0   
state_init[76,2] = 100.0
state_init[1,:] .= [K,0]
state_init[end,:] .= [0,0]

state = deepcopy(state_init)
state_plus = zeros(size(state_init)) # state at demes i+1 instead of i (used for derivatives)
state_minus = zeros(size(state_init)) # state at demes i-1 instead of i (used for derivatives)

function sim!(state_init::Matrix{Float64}, state::Matrix{Float64},
              T::Int64, dt::Float64, N::Int64, M::Int64, K::Int64,
              hist_data::Array{Int64,3}, g::Normal{Float64})

    @inbounds @floop for n in 1:N
        state .= deepcopy(state_init) # initialize state
        @inbounds for t in 1:T
            
            state_plus .= circshift(state, -1) # make plus state
            state_plus[1,:] .= [0,0] # fix boundary conditions
            state_minus .= circshift(state, 1) # make minus state
            state_minus[end,:] .= [0,0] # fix boundary conditions
            state_shift = circshift(state, (0,1)) 
            # make state where each deme has a vector 
            # (# mutants, # wild-types) instead of 
            # (# wild-types, # mutants)

            ######################################
            # propagate state using Euler-Murayama method and
            # restrict number of cells in a deme to be in the range [0,K]
            # using clamp(). clamp() also prevents imaginary numbers from 
            # a negative number under the sqrt().

            state .= clamp.(state .+ 
            dt .* (r_wm .* state .* (K .- state .- state_shift) .+ 
            K .* (state_plus .- 2.0 .* state .+ state_minus)) .+ 
            sqrt.(clamp.(
            6 .* state .* (K .- state) .+ 
            (K .- 2.0 .* state) .* (state_plus .- 2.0 .* state .+ 
            state_minus) .- r_wm .* state .* (K .- state .- state_shift), 
            0.0, 1.0*K*K)) .* 
            rand(g,M+2), 0.0, 1.0*K) 
            ######################################

        end
    end
end

sim!(state_init, state, T, dt, N, M, K, hist_data, g)


... the rest of the code is analysis and not the reason the code is slow.

Put all the code in a function and call that function. Global variables (ones defines in the REPL or not inside function) are too dynamic in nature to be properly optimized for. See https://docs.julialang.org/en/v1/manual/performance-tips/ — Dan Getz, Nov 02 '22 at 02:40
It helped a bit :) It went from about 50 minutes to about 40 minutes runtime. I am hoping there is still something I can do. — Jason M Gray, Nov 02 '22 at 03:35
There is still much to optimize after using suggestions in answer. First off, the `deepcopy` is unnecessary as the values are assigned to an existing array. Furthermore, there is at least 3 copy operations on the `state` which can probably be reduced to at most 1. Perhaps giving shorter variable names will make the code look more compact and easier to reason about - for example, the propagation step at each loop has a long multi-line expression which will become shorter with small variables names. — Dan Getz, Nov 02 '22 at 20:17
It seems to be coming together now :) Thank you all so much for the help! I've changed the way the code is implemented by referencing state[2:end-1,1], state[1:end-2,1], and state[3:end,1] instead of state, state_minus, and state_plus. I think this solves a lot of the slow down. — Jason M Gray, Nov 03 '22 at 00:25
Make sure to use `@views` when you do that. `state[2:end-1,1]` allocates new memory to contain that part of the array. Placing `@views` at the beginning of the line changes such array-slice accesses to use pieces of the original array itself (providing "view"s into the original array), so avoids that allocation. — Sundar R, Nov 03 '22 at 06:08

Sundar R · Accepted Answer · 2022-11-02T11:51:15.190

Even though you're pre-allocating state_plus and state_minus, memory is being allocated inside the for loop since you're using circshift instead of circshift!. circshift allocates new memory regardless of the fact that it's ultimately being assigned to an existing pre-allocated array. Doing that allocation 300 million times is bound to be costly!

Try

function sim!(state_init::Matrix{Float64}, state::Matrix{Float64},
              T::Int64, dt::Float64, N::Int64, M::Int64, K::Int64,
              hist_data::Array{Int64,3}, g::Normal{Float64})

    @inbounds @floop for n in 1:N
        state .= deepcopy(state_init) # initialize state
        state_plus = zeros(size(state_init)) # state at demes i+1 instead of i (used for derivatives)
        state_minus = zeros(size(state_init)) # state at demes i-1 instead of i (used for derivatives)
        state_shift = zeros(size(state_init)) 

        for t in 1:T
            
            circshift!(state_plus, state, -1) # make plus state
            state_plus[1,:] .= [0,0] # fix boundary conditions
            circshift!(state_minus, state, 1) # make minus state
            state_minus[end,:] .= [0,0] # fix boundary conditions
            circshift!(state_shift, state, (0,1))

and

function sim!(state_init::Matrix{Float64}, state::Matrix{Float64},
              T::Int64, dt::Float64, N::Int64, M::Int64, K::Int64,
              hist_data::Array{Int64,3}, g::Normal{Float64})

    state_plus = zeros(size(state_init)) # state at demes i+1 instead of i (used for derivatives)
    state_minus = zeros(size(state_init)) # state at demes i-1 instead of i (used for derivatives)
    state_shift = zeros(size(state_init)) 
    @inbounds for n in 1:N
        state .= deepcopy(state_init) # initialize state
        for t in 1:T
            
            circshift!(state_plus, state, -1) # make plus state
            state_plus[1,:] .= [0,0] # fix boundary conditions
            circshift!(state_minus, state, 1) # make minus state
            state_minus[end,:] .= [0,0] # fix boundary conditions
            circshift!(state_shift, state, (0,1))

The second version doesn't use @floop, but that allows it to not have to initialize state_plus and others N times, so it may be the case that it's faster for your actual N. Best to try both and find out!

I see, thank you :) I've changed the way the code is implemented by referencing state[2:end-1,1], state[1:end-2,1], and state[3:end,1] instead of state, state_minus, and state_plus. I think this solves a lot of the slow down. — Jason M Gray, Nov 03 '22 at 00:26

Julia Stochastic Differential Equation Very Slow

1 Answers1