I am trying to solve the following nonlinear system of differential equation with the explicit Euler method:
x' = f1(x,y),
y' = f2(x,y)
And I know the fact that the curve corresponding to the solution must connect (x_{initial},y_{initial}) to (0,1) in the x-y plane, but the obtained curve stops prematurely at around (0.17,0.98). I tried to vary the parameters but again I can't push that value any further towards (0,1). First, I thought my equations becomes stiff towards the end point; now it doesn't seem to be the case when I read about the stiff ODEs. What might be the problem?
The code I wrote in python is:
import math
import numpy as np
import matplotlib.pyplot as plt
q=1
#my f1 and f2 functions:
def l(lna,x,y,m,n,xi,yi):
return n *m**(-1)*(np.divide((yi**2)*(np.float64(1)-np.power(x,2)-np.power(y,2))*np.exp(3*(lna-lnai)),(y**2)*(1-xi**2-yi**2)))**(-1/n)
def f1 (x,y,l):
return -3*x + l*np.sqrt(3/2)* y**2+ 3/2 *x*(2*(x**2)+q*(1-x**2-y**2))
def f2 (x,y,l):
return -l*np.sqrt(3/2) *y*x + 3/2 *y*(2*x**2+q*(1-x**2-y**2))
#my code for the explicit Euler:
def e_E(xa,xb,dlna,m,n,xi,yi):
N = int(round((lnaf-lnai)/dlna))
lna = np.linspace(0, N*dlna, N+1)
x = np.empty(N+1)
y = np.empty(N+1)
x[0],y[0] = xi,yi
for i in range(N):
sd = l(lna[i],x[i],y[i],m,n,xi,yi)
x[i+1] = x[i] + dlna * f1(x[i],y[i],sd)
y[i+1] = y[i] + dlna * f2(x[i],y[i],sd)
return x,y,lna
#range for the independent variable (in my case it is lna)
lnai = np.float64(0)
lnaf = np.float64(15)
#step size
dlna = np.float64(1e-3)
#initial conditions
yi = np.float64(1e-5)
xi = 0
x1,y1,lna1 = e_E(lnai, lnaf, dlna, np.float64(0.1), np.float64(2), xi, yi)
plt.plot(x1,y1,'b',label = ('x1'))
plt.legend()
plt.grid()
plt.ylabel('y')
plt.xlabel('x')
plt.show()
My solution in the x-y plane:
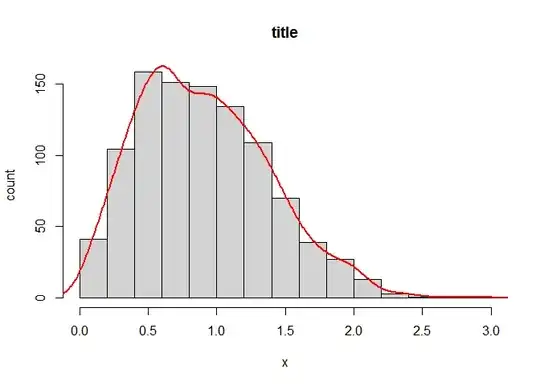
Full/correct solution: