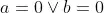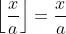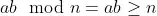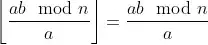Correctness of multiplication with overflow detection

Question

The following C++ template detects overflows from multiplying two unsigned integers.

template<typename UInt> UInt safe_multiply(UInt a, UInt b) {
    UInt x = a * b; // x := ab mod n, for n := 2^#bits > 0
    if (a != 0 && x / a != b)
        cerr << "Overflow for " << a << " * " << b << "." << endl;
    return x;
}

Can you give a proof that this algorithm detects every potential overflow, regardless of how many bits UInt uses?

The case
$a=0\lor b=0$

cannot result in overflows, so we can consider
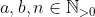$a,b,n\in\mathbb{N}_{>0}$ .

It seems that the correctness proof boils down to leading
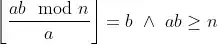
$\left\lfloor\frac{ab \mod n}{a}\right\rfloor=b~\land~ab\ge n$

to a contradiction, since x / a actually means 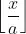$\left\lfloor\frac{x}{a}\right\rfloor$ .

When assuming
$\left\lfloor\frac{x}{a}\right\rfloor=\frac{x}{a}$

, this leads to the straightforward consequence
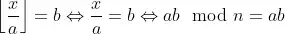
$\left\lfloor\frac{x}{a}\right\rfloor=b\Leftrightarrow\frac{x}{a}=b\Leftrightarrow ab \mod n=ab$

thus
$ab\mod n=ab\ge n$

which contradicts n > 0.

So it remains to show
$\left\lfloor\frac{ab \mod n}{a}\right\rfloor=\frac{ab \mod n}{a}$

or there must be another way.

If the last equation is true, WolframAlpha fails to confirm that (also with exponents).
However, it asserts that the original assumptions have no integer solutions, so the algorithms seems to be correct indeed.
But it doesn't provide an explanation. So why is it correct?

I am looking for the smallest possible explanation that is still mathematically profound, ideally that it fits in a single-line comment. Maybe I am missing something trivial, or the problem is not as easy as it looks.

On a side note, I used Codecogs Equation Editor for the LaTeX markup images, which apparently looks bad in dark mode, so consider switching to light mode or, if you know, please tell me how to use different images depending on the client settings. It is just \bg{white} vs. \bg{black} as part of the image URLs.

@Elliott Thanks for the notification. I will update the images to have a white background. — xamid, Nov 08 '22 at 04:45
That last equation is definitely false, and it's false so often that you can plug in basically any random set of constants and see it fail — harold, Nov 08 '22 at 05:17

Elliott · Accepted Answer · 2022-11-08T07:12:03.243

To be clear, I'll use the multiplication and division symbols (*, /) mathematically.

Also, for convenience let's name the set N = {0, 1, ..., n - 1}.

Let's clear up what unsigned multiplication is:
Unsigned multiplication for some magnitude, n, is a modular n operation on unsigned-n inputs (inputs that are in N) that results in an unsigned-n output (ie. also in N).
In other words, the result of unsigned multiplication, x, is x = a*b (mod n), and, additionally, we know that x,a,b are in N.
It's important to be able to expand many modular formulas like so: x = a*b - k*n, where k is an integer - but in our case x,a,b are in N so this implies that k is in N.

Now, let's mathematically say what we're trying to prove:
Given positive integers, a,n, and non-negative integers x,b, where x,a,b are in N, and x = a*b (mod n), then a*b >= n (overflow) implies floor(x/a) != b.

Proof:

If overflow (a*b >= n) then x >= n - k*n = (1 - k)*n (for k in N),
As x < n then (1 - k)*n < n, so k > 0.
This means x <= a*b - n.

So, floor(x/a) <= floor([a*b - n]/a) = floor(a*b/a - n/a) = b - floor(n/a) <= b - 1,
Abbreviated: floor(x/a) <= b - 1
Therefore floor(x/a) != b

Could you elaborate why `x <= a*b - n` holds in case of an overflow? This seems a crucial part that I missed. — xamid, Nov 08 '22 at 05:30
Ah yes, so what you meant is using the definition of `mod` by which `x = a*b mod n` means there is an integer `k` such that `x = k*n + a*b` holds, and since `x < n <= a*b` we have `k <= -1`, thus `x <= a*b - n`. Your proof is correct. I will accept it if there won't be any shorter ways soon. — xamid, Nov 08 '22 at 06:36

score -2 · Answer 2 · answered Nov 08 '22 at 08:11

-2

The multiplication gives either the mathematically correct result, or it is off by some multiple of 2^64. Since you check for a=0, the division always gives the correct result for its input. But in the case of overflow, the input is off by 2^64 or more, so the test will fail as you hoped.

The last bit is that unsigned operations don’t have undefined behaviour except for division by zero, so your code is fine.

answered Nov 08 '22 at 08:11

gnasher729

51,477
5
75
98

1. The algorithm is not limited to 64-bit integers. 2. It is to show precisely why `x / a != b` holds whenever an overflow occured (also considering that implicit `floor()`). You gave a sketch but that's not a proof. For instance, it doesn't clarify why any two fitting numbers `a,b` multiplied modulo `n` divided by `a` cannot be floored to equal `b`. – xamid Nov 08 '22 at 09:37

Correctness of multiplication with overflow detection

2 Answers2