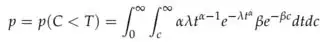1

We have a function. t ~ Weibull(alpha, lambda) and c ~ Exponential(beta):

enter image description here

Given p = 0.10, alpha = 1, lambda = 4. Find the value of beta.

We want to integrate this function for t then to c. Then find the value of beta where integral equals to p using uniroot function.

See the code below:

alpha = 1
lambda = 4
p = 0.10
func1 <- function(t, c, beta) {alpha * lambda * exp(-lambda * t^ alpha)*
                           beta * exp(- beta * c) }
func2 <- function(c, beta){integrate(func1, lower = c, upper = Inf, c=c, 
beta=beta)}
func3 <- function(beta){integrate(func2, lower = 0, upper = Inf, beta = 
beta)$value - cen.p}
uniroot(func3 ,lower = 0.001, upper = 10, extendInt = "yes")$root

However it throws the error:

Error in integrate(func1, lower = c, upper = Inf, c = c, beta = beta) : length(lower) == 1 not TRUE

Answer should be 0.444

Artem
  • 3,304
  • 3
  • 18
  • 41
Parviz Shahmirzalou
  • 13
  • 3
  • What did you try? Where did you get stuck? – Rogue Nov 30 '22 at 15:46
  • Thanks Rogue. Now, I add my code in R-studio. This code report that: length(lower) == 1 is not TRUE – Parviz Shahmirzalou Nov 30 '22 at 16:31
  • Please clarify your specific problem or provide additional details to highlight exactly what you need. As it's currently written, it's hard to tell exactly what you're asking. – Community Nov 30 '22 at 19:06
  • Thanks. I want to solve attached function to get "B" or beta of exponential distribution. we set alpha=1, lambda=4, p=0.10, beta=? . I write code in rstudio but it's not correct. – Parviz Shahmirzalou Nov 30 '22 at 20:25

1 Answers1

0

I corrected typos (substituted cen.p to p) and vectorized function arguments for func2 and func3, since the integrate function returns one value (scalar). However as a first argument integrate should accept vector of numeric values, not a scalar.

alpha <- 1
lambda <- 4
p <- 0.10
func1 <- function(t, c, beta)
  alpha * lambda * t^(alpha - 1) * exp(-lambda * t^alpha) * beta * exp(-beta * c)

func2 <- function(c, beta)
  integrate(func1, lower = c, upper = Inf, c = c, beta = beta)$value)

func3 <- function(beta)
  integrate(Vectorize(func2), lower = 0, upper = Inf, beta = beta)$value - p

uniroot(Vectorize(func3), lower = 0.001, upper = 10, extendInt = "yes")$root

Output:

[1] 0.4444242.
Artem
  • 3,304
  • 3
  • 18
  • 41
  • thanks a lot. One note: This code for a=0.25 report error. why? Error in integrate(Vectorize(func2), lower = 0, upper = Inf, beta = beta) : the integral is probably divergent – Parviz Shahmirzalou Dec 02 '22 at 10:10
  • You ommited t^(alpha - 1) multiplier from function, code corrected. Please check. – Artem Dec 02 '22 at 11:30