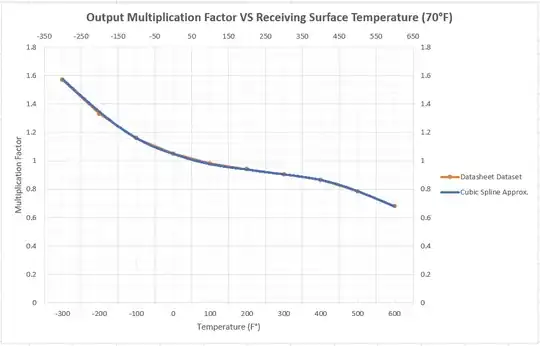
I am working on a function in C programming and would like to create a function based off of the given data points but I cannot seem to get something that fits this curve. See graph here:
My program will primarily use this function in the 0-500°F range so it is important that this range is accurate.
Using this graph I have determined the data points to be approximately:
Temp(F), Factor
(-300, 1.57)
(-200, 1.33)
(-100, 1.16)
(0, 1.05)
(100, 0.98)
(200, 0.94)
(300, 0.915)
(400, 0.865)
I have found that y = 0.00000244x^2 -0.001x + 1.05 is a close fit for the -300-100°F range but gets very bad for x>100°F values.
y = 1.6904761904745*10^-6 x^2 - 0.00109048x + 1.0628 seems to be closer.
I figure that I need a cubic function to model this well, but I can't figure out what it would be. Any recommendations? I was also thinking that I could model T<200°F & T>200°F as separate functions.
EDIT1 I have found a set of linear piecewise functions that fit the dataset, still probably inaccurate for the 400-500°F range.
1.) y=-0.0024x + 0.85 {-300< x <-200}
2.) y=-0.0017x + 0.99 {-200< x <-100}
3.) y=-0.0011x + 1.05 {-100< x < 0}
4.) y=-0.0007x + 1.05 {0 < x <100}
5.) y=-0.0004x + 1.02 {100 < x < 200}
6.) y=-0.00025x + 0.99 {200 < x < 300}
7.) y=-0.0005x + 1.065 {300< x < 400}
8.) y=-0.00065x + 1.125 {400< x < 500} *estimated factor to be 0.8 @ 500°F*
EDIT2
I was able to model this pretty well with the help of JJacquelin's answer below. I have settled on using a piecewise set of two functions:
1.) y = 0.83583 + 0.218653e^{-0.00404x} {-400 < x < 185}
2.) y = -0.0000014x^2 + 0.000465x + 0.9027 {185 < x < 500}
Interactive graph here
EDIT 3:
JAlex Has a good point about using Cubic Spline interpolation. This is the method I ended up using. I found an Arduino library and adapted it to my project. sakov/csa-c (Cubic Spline Approximation
You can see the the cubic spline approximation (CSA) fits the original dataset quite well. Keep in mind the point for T=500°F & T=600°F were estimated using equation 2 from EDIT2.