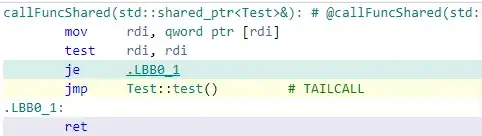
This is a standard benchmark problem for minimum flight time.
This is a very standard problem. I am trying to solve it in gekko, but it is neither converging to local minima nor global, here is the code. I followed the set up from the Jennings problem but still, if anybody can help, that would be very nice.
from gekko import GEKKO
import numpy as np
import matplotlib.pyplot as plt
import math
m = GEKKO()
nt = 501
tm = np.linspace(0,1,nt)
m.time = tm
x1=m.Var(value=-2.5)
x2=m.Var(value=0)
u=m.MV(value=1,lb=0,ub=2*math.pi)
p = np.zeros(nt)
p[-1] = 1.0
final = m.Param(value=p)
tf = m.FV(value=0,lb=0.1,ub=100.0)
tf.STATUS = 1
if x2.value>1:
m.Equation(x1.dt()==((1+(x2-1)**2)*m.cos(u)*tf))
m.Equation(x2.dt()==((1+(x2-1)**2)*m.sin(u)*tf))
else:
m.Equation(x1.dt()==(m.cos(u)*tf))
m.Equation(x2.dt()==(m.sin(u)*tf))
#m.Equation(x1*final<=3)
#m.Equation(x2*final<=0)
m.Minimize(tf)
m.options.IMODE = 6
m.solve()
tm = tm * tf.value[0]
plt.figure(1)
plt.plot(tm,x1.value,'k-',lw=2,label=r'$x_1$')
plt.plot(tm,x2.value,'b-',lw=2,label=r'$x_2$')
plt.plot(tm,u.value,'r--',lw=2,label=r'$u$')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()