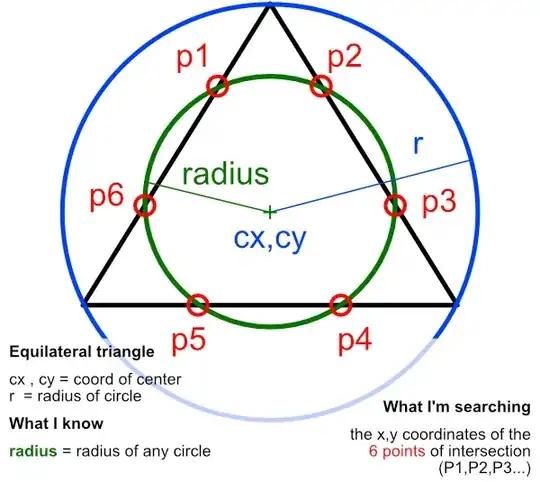
function setup() {
createCanvas(500, 500);
const cx = width / 2;
const cy = height / 2;
const r = 250; // taille du triangle
const radius = 180; // externe
noFill();
strokeWeight(3);
stroke(0, 0, 0);
drawTriangle(cx, cy, r);
strokeWeight(1);
stroke(0, 0, 255);
circle(cx, cy, r * 2);
strokeWeight(2);
stroke(8, 115, 0);
circle(cx, cy, radius * 2);
noStroke();
fill(215, 0, 0);
// dx = sqrt(Math.pow(r / 2, 2) - Math.pow(r / 2, 2 / 4));
dx = sqrt(radius * radius - (r * r) / 4);
p4x = dx;
p4y = r / 2;
circle(cx + p4x, cy + p4y, 20);
text("p4", cx + p4x, cy + p4y + 30);
p5x = -dx;
p5y = r / 2;
circle(cx + p5x, cy + p5y, 20);
text("p5", cx + p5x - 10, cy + p5y + 30);
p6x = p4x * (-1 / 2) - p4y * (sqrt(3) / 2);
p6y = p4x * (sqrt(3) / 2) + p4y * (-1 / 2);
circle(cx + p6x, cy + p6y, 20);
text("p6", cx + p6x - 30, cy + p6y);
p2x = p6x * (-1 / 2) - p6y * (sqrt(3) / 2);
p2y = p6x * (sqrt(3) / 2) + p6y * (-1 / 2);
circle(cx + p2x, cy + p2y, 20);
text("p2", cx + p2x + 10, cy + p2y - 10);
p1x = p5x * (-1 / 2) - p5y * (sqrt(3) / 2);
p1y = p5x * (sqrt(3) / 2) + p5y * (-1 / 2);
circle(cx + p1x, cy + p1y, 20);
text("p1", cx + p1x - 20, cy + p1y - 10);
p3x = p1x * (-1 / 2) - p1y * (sqrt(3) / 2);
p3y = p1x * (sqrt(3) / 2) + p1y * (-1 / 2);
circle(cx + p3x, cy + p3y, 20);
text("p3", cx + p3x + 20, cy + p3y - 10);
noFill();
stroke(0, 255, 255);
triangle(cx + p2x, cx + p2y, cx + p4x, cx + p4y, cx + p6x, cx + p6y);
stroke(255, 0, 255);
// prettier-ignore
triangle(
cx + p1x, cx + p1y,
cx + p3x, cx + p3y,
cx + p5x, cx + p5y,
)
}
function drawTriangle(cx, cy, radius) {
noFill();
trianglePoints = [];
for (var i = 0; i < 3; i++) {
var x = cx + radius * cos((i * TWO_PI) / 3.0 - HALF_PI);
var y = cy + radius * sin((i * TWO_PI) / 3.0 - HALF_PI);
trianglePoints[i] = {
x,
y,
};
}
triangle(
trianglePoints[0].x,
trianglePoints[0].y,
trianglePoints[1].x,
trianglePoints[1].y,
trianglePoints[2].x,
trianglePoints[2].y
);
}
<script src="https://cdnjs.cloudflare.com/ajax/libs/p5.js/1.5.0/p5.min.js"></script>