In ggplot, how to fill area between two normal curves

Question

I have two normal curves and I want to fill the right area between both curves, so left curve is inferior y limit and right curve is superior y limit. To plot the curves I am using stat_function() so ggplot draws the curve without defining an y-column in aes(). I have drawn the fill area between the curve and the X axis, but I need the area between both curves and the trick of emptying the left curve with NA doesn't seem to work as I expected.

The code to generate the plot is in a function as I need to plot several different couples of normal curves.

How can I do that?

library(ggplot2)
library(ggthemes)

graf_normal <- function(Xmedia1, Xdt1, Xmedia2, Xdt2) {

  Xmin1 <- Xmedia1-4*Xdt1
  Xmax1 <- Xmedia1+4*Xdt1

  Xmin2 <- Xmedia2-4*Xdt2
  Xmax2 <- Xmedia2+4*Xdt2

  Ymax1 <- max(dnorm(Xmedia1, Xmedia1, Xdt1))
  Ymax2 <- max(dnorm(Xmedia2, Xmedia2, Xdt2))

  Xmin <- min(Xmin1, Xmin2)
  Xmax <- max(Xmax1, Xmax2)

  ggplot(data.frame(X = c(Xmin, Xmax)), aes(x = X)) +
  geom_hline(yintercept = 0, colour = "grey", linewidth = 1) +
  stat_function(fun = dnorm, 
              args = c(Xmedia1, Xdt1), 
              linewidth = 1, 
              colour = "grey") +
  stat_function(fun = dnorm, 
              args = c(Xmedia2, Xdt2), 
              linewidth = 1, 
              colour = "black") +
  geom_segment(aes(x = Xmedia1, y = 0, xend = Xmedia1, yend = Ymax1), 
             linetype = "dashed", 
             linewidth = 0, 
             colour = "grey") +
  geom_segment(aes(x = Xmedia2, y = 0, xend = Xmedia2, yend = Ymax2), 
             linetype = "dashed", 
             linewidth = 0, 
             colour = "black") +
  ####################################################################
  stat_function(fun = dnorm,
            args = c(Xmedia2, Xdt2),
            xlim = c(Xmedia2+1.5*Xdt2,Xmax2),
            geom = "area",
            fill = "red",
            alpha = 0.5) +
  stat_function(fun = dnorm,
              args = c(Xmedia1, Xdt1),
              xlim = c(Xmedia1,Xmax1),
              geom = "area",
              fill = NA,
              alpha = 0.01) +

  ##################################################################

  theme(
    line = element_blank(),
    axis.line.y = element_blank(),
    axis.text.x = element_blank(),
    axis.text.y = element_blank(),
    axis. Ticks = element_blank(),
    axis.title.x = element_blank(),
    axis.title.y = element_blank(),
    legend. Position = "none",
    panel. Grid = element_blank(),
    panel. Background = element_rect(fill = "lightgray", colour = NA),
 ) +
 xlim(c(Xmin, Xmax)) 
}

g1 <- graf_normal(250, 7, 253, 7)

g1

The plot of both curves I get is this:

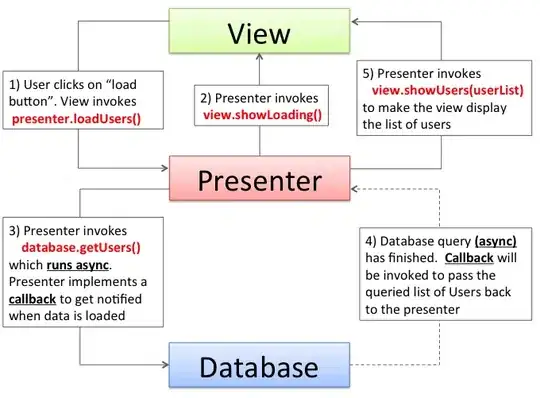
Thanks,

EDIT: Using @stephan's code and playing with data filtering, I've been able to do this, easier using geom_ribbon():

Cool way of differencing overlapping zones! Complete code:

library(ggplot2)

graf_normal <- function(Xmedia1, Xdt1, Xmedia2, Xdt2, n = 1000) {
  x1 <- Xmedia1 + 4 * Xdt1 * seq(-1, 1, length. Out = n)
  x2 <- Xmedia2 + 4 * Xdt2 * seq(-1, 1, length. Out = n)

  dat <- data. Frame(
    x = union(x1, x2)
  )
  dat$y1 <- dnorm(dat$x, Xmedia1, Xdt1)
  dat$y2 <- dnorm(dat$x, Xmedia2, Xdt2)

  Ymax1 <- dnorm(Xmedia1, Xmedia1, Xdt1)
  Ymax2 <- dnorm(Xmedia2, Xmedia2, Xdt2)

  ggplot(dat, aes(x)) +
    geom_hline(yintercept = 0, colour = "grey", linewidth = 1) +
    geom_ribbon(
      data =  subset(dat, x >= Xmedia2 + 1.5 * Xdt2),
      aes(ymin = y1, ymax = y2),
      fill = "red", alpha = 0.8
    ) +
    geom_ribbon(
      data =  subset(dat, (x <= Xmedia2 + 1.5 * Xdt2) & (y2 > y1)),
      aes(ymin = y1, ymax = y2),
      fill = "red", alpha = 0.2
    ) +
    geom_ribbon(
      data = subset(dat, x <= Xmedia1 - 1.5 * Xdt2),
      aes(ymin = y1, ymax = y2),
      fill = "blue", alpha = 0.8
    ) +
    geom_ribbon(
      data = subset(dat, (x <= Xmedia2 ) & (y1 > y2)),
      aes(ymin = y1, ymax = y2),
      fill = "blue", alpha = 0.2
    ) +
    annotate(
      geom = "segment",
      x = c(Xmedia1, Xmedia2), y = 0,
      xend = c(Xmedia1, Xmedia2), yend = c(Ymax1, Ymax2),
      linetype = "dashed",
      linewidth = 1,
      colour = c("grey", "black")
    ) +
    geom_line(aes(y = y1), linewidth = 1, colour = "grey") +
    geom_line(aes(y = y2), linewidth = 1, colour = "black") +
    theme(
      line = element_blank(),
      axis.line.y = element_blank(),
      axis. Text = element_blank(),
      axis. Ticks = element_blank(),
      axis. Title = element_blank(),
      legend. Position = "none",
      panel. Grid = element_blank(),
      panel. Background = element_rect(fill = "lightgray", colour = NA),
    )
}

graf_normal(250, 7, 253, 7)

However, the code doesn't work for all curves, working on it!:

graf_normal(250, 7, 253, 3)

stefan · Accepted Answer · 2023-02-20T00:47:06.783

One option to fill the area between the normal curves would be to use ggh4x::stat_difference which however requires to compute the values for the densities manually and drawing via geom_line instead of relying on stat_function():

library(ggplot2)
library(ggh4x)
graf_normal <- function(Xmedia1, Xdt1, Xmedia2, Xdt2, n = 101) {
  x1 <- Xmedia1 + 4 * Xdt1 * seq(-1, 1, length.out = n)
  x2 <- Xmedia2 + 4 * Xdt2 * seq(-1, 1, length.out = n)
  
  dat <- data.frame(
    x = union(x1, x2)
  )
  dat$y1 <- dnorm(dat$x, Xmedia1, Xdt1)
  dat$y2 <- dnorm(dat$x, Xmedia2, Xdt2)

  Ymax1 <- dnorm(Xmedia1, Xmedia1, Xdt1)
  Ymax2 <- dnorm(Xmedia2, Xmedia2, Xdt2)

  ggplot(dat, aes(x)) +
    geom_hline(yintercept = 0, colour = "grey", linewidth = 1) +
    ggh4x::stat_difference(
      data = ~ subset(.x, x >= Xmedia2 + 1.5 * Xdt2),
      aes(ymin = y1, ymax = y2)
    ) +
    annotate(
      geom = "segment",
      x = c(Xmedia1, Xmedia2), y = 0,
      xend = c(Xmedia1, Xmedia2), yend = c(Ymax1, Ymax2),
      linetype = "dashed",
      linewidth = 1,
      colour = c("grey", "black")
    ) +
    geom_line(aes(y = y1), linewidth = 1, colour = "grey") +
    geom_line(aes(y = y2), linewidth = 1, colour = "black") +
    scale_fill_manual(values = c(scales::alpha("red", .5), "transparent")) +
    theme(
      line = element_blank(),
      axis.line.y = element_blank(),
      axis.text = element_blank(),
      axis.ticks = element_blank(),
      axis.title = element_blank(),
      legend.position = "none",
      panel.grid = element_blank(),
      panel.background = element_rect(fill = "lightgray", colour = NA),
    )
}

graf_normal(250, 7, 253, 7)

EDIT Actually stat_differnce is not really needed for your case. Was thinking too complicated. As @JuanRiera mentioned in his comment, we could fill the area using a geom_ribbon:

library(ggplot2)

graf_normal <- function(Xmedia1, Xdt1, Xmedia2, Xdt2, n = 101) {
  x1 <- Xmedia1 + 4 * Xdt1 * seq(-1, 1, length.out = n)
  x2 <- Xmedia2 + 4 * Xdt2 * seq(-1, 1, length.out = n)

  dat <- data.frame(
    x = union(x1, x2)
  )
  dat$y1 <- dnorm(dat$x, Xmedia1, Xdt1)
  dat$y2 <- dnorm(dat$x, Xmedia2, Xdt2)

  Ymax1 <- dnorm(Xmedia1, Xmedia1, Xdt1)
  Ymax2 <- dnorm(Xmedia2, Xmedia2, Xdt2)

  ggplot(dat, aes(x)) +
    geom_hline(yintercept = 0, colour = "grey", linewidth = 1) +
    geom_ribbon(aes(ymin = y1, ymax = y2),
      data = subset(dat, x >= Xmedia2 + 1.5 * Xdt2),
      fill = "red", alpha = 0.5
    ) +
    annotate(
      geom = "segment",
      x = c(Xmedia1, Xmedia2), y = 0,
      xend = c(Xmedia1, Xmedia2), yend = c(Ymax1, Ymax2),
      linetype = "dashed",
      linewidth = 1,
      colour = c("grey", "black")
    ) +
    geom_line(aes(y = y1), linewidth = 1, colour = "grey") +
    geom_line(aes(y = y2), linewidth = 1, colour = "black") +
    theme(
      line = element_blank(),
      axis.line.y = element_blank(),
      axis.text = element_blank(),
      axis.ticks = element_blank(),
      axis.title = element_blank(),
      legend.position = "none",
      panel.grid = element_blank(),
      panel.background = element_rect(fill = "lightgray", colour = NA),
    )
}

graf_normal(250, 7, 253, 7)

Thanks a lot, Stefan, your code adds some nice ideas like the annotation better coded. However the use of another library is not ideal for the environment where I must deploy the solution. I will think about your solution and r2evans. — Juan Riera, Feb 19 '23 at 18:50
Hi Juan. Sure. Feel free to choose whatever approach fits your needs best. And of course could you mix both, i.e. you could replace ggh4x::stat_difference in my code with the `geom_polygon` approach by @r2evans. — stefan, Feb 19 '23 at 18:59
I wanted to edit but I can't after 5 min lol - your code adds MANY nice ideas! — Juan Riera, Feb 19 '23 at 19:02
Stefan, I just checked that `ggh4x::stat_difference(` can be directly replaced by `geom_ribbon(` and the code works nicely same way — Juan Riera, Feb 19 '23 at 22:40
BTW, could you please explain the use of tilde in `~ subset(.x, x >= Xmedia2 + 1.5 * Xdt2)`? Can't find anything about it — Juan Riera, Feb 19 '23 at 23:18
Haha. Yeah, of course. Was thinking too complicated. For your case we could simply use `geom_ribbon`. `stat_difference` is only needed if we want to fill starting at the intersection point or in case that we want to fill the area between the densities over the whole range of data. Concerning`~ subset(.x, x >= Xmedia2 + 1.5 * Xdt2)`: It subsets the data passed to `ggplot()`. In your case we could simply do `subset(dat, ...)`. But using this notation is handy in case where we do something like `dat %>% filter(...) %>% ggplot(...)`. — stefan, Feb 20 '23 at 00:42
Well, believe it or not, you anticipated my next question: ¿how to fill from intersection? Just by not doing a subset and using the whole dataset `dat`: *voilà*, done! This thing it's being fun :) — Juan Riera, Feb 20 '23 at 09:02
My doubt it's about tilde notation, with the use of tilde before `~subset` and not with `subset` function - I have never used tilde before a function and It's not clear to me what's it used for. Thanks! — Juan Riera, Feb 20 '23 at 09:15
Hi Juan. You find the `~` notation all over the tidyverse. Basically `~ f(.x)` is the same as `function(.x) f(.x)` just shorter. See e.g. https://stackoverflow.com/questions/67643144/where-is-the-purrr-operator-documented for some references. — stefan, Feb 20 '23 at 12:24

r2evans · Answer 2 · 2023-02-19T18:46:38.540

One way is using a geom_polygon instead of stat_function.

Add this to your function, before the ggplot():

  poly <- data.frame(xs = seq(Xmedia2+1.5*Xdt2, Xmax2, length.out = n)) |>
    transform(
      y1 = dnorm(xs, Xmedia1, Xdt1),
      y2 = dnorm(xs, Xmedia2, Xdt2)
    ) |>
    with(data.frame(X = c(xs, rev(xs)), Y = c(y1, rev(y2))))

And then replace your both of your second two stat_function calls with a single

  geom_polygon(aes(X, Y), data = poly,
               fill = "red", alpha = 0.5) +

Full source:

graf_normal <- function(Xmedia1, Xdt1, Xmedia2, Xdt2, n = 20) {

  Xmin1 <- Xmedia1-4*Xdt1
  Xmax1 <- Xmedia1+4*Xdt1

  Xmin2 <- Xmedia2-4*Xdt2
  Xmax2 <- Xmedia2+4*Xdt2

  Ymax1 <- max(dnorm(Xmedia1, Xmedia1, Xdt1))
  Ymax2 <- max(dnorm(Xmedia2, Xmedia2, Xdt2))

  Xmin <- min(Xmin1, Xmin2)
  Xmax <- max(Xmax1, Xmax2)

  poly <- data.frame(xs = seq(Xmedia2+1.5*Xdt2, Xmax2, length.out = n)) |>
    transform(
      y1 = dnorm(xs, Xmedia1, Xdt1),
      y2 = dnorm(xs, Xmedia2, Xdt2)
    ) |>
    with(data.frame(X = c(xs, rev(xs)), Y = c(y1, rev(y2))))

  ggplot(data.frame(X = c(Xmin, Xmax)), aes(x = X)) +
  geom_hline(yintercept = 0, colour = "grey", linewidth = 1) +
  geom_polygon(aes(X, Y), data = poly,
               fill = "red", alpha = 0.5) +
  stat_function(fun = dnorm, 
              args = c(Xmedia1, Xdt1), 
              linewidth = 1, 
              colour = "grey") +
  stat_function(fun = dnorm, 
              args = c(Xmedia2, Xdt2), 
              linewidth = 1, 
              colour = "black") +
  geom_segment(aes(x = Xmedia1, y = 0, xend = Xmedia1, yend = Ymax1), 
             linetype = "dashed", 
             linewidth = 0, 
             colour = "grey") +
  geom_segment(aes(x = Xmedia2, y = 0, xend = Xmedia2, yend = Ymax2), 
             linetype = "dashed", 
             linewidth = 0, 
             colour = "black") +
  ####################################################################
  # stat_function(fun = dnorm,
  #           args = c(Xmedia2, Xdt2),
  #           xlim = c(Xmedia2+1.5*Xdt2,Xmax2),
  #           geom = "area",
  #           fill = "red",
  #           alpha = 0.5) +
  # stat_function(fun = dnorm,
  #             args = c(Xmedia1, Xdt1),
  #             xlim = c(Xmedia1,Xmax1),
  #             geom = "area",
  #             fill = NA,
  #             alpha = 0.01) +
  ##################################################################
  theme(
    line = element_blank(),
    axis.line.y = element_blank(),
    axis.text.x = element_blank(),
    axis.text.y = element_blank(),
    axis.ticks = element_blank(),
    axis.title.x = element_blank(),
    axis.title.y = element_blank(),
    legend.position = "none",
    panel.grid = element_blank(),
    panel.background = element_rect(fill = "lightgray", colour = NA),
    ) +
    xlim(c(Xmin, Xmax)) 

}

Note: I chose to move the geom_polygon to much earlier in the plot-stack so that the dnorm-lines would be "on top" of the red area. Whether this is important depends on your context and rendering engine.

I like in this solution that code is less modified, even if my code is not too efficient, I think it it may be clearer in the context I will use it, with people learning to code. I see from both answers that I need to generate the Y values, and I can't rely on included functions. Not a major problem, in any case. Thanks a lot, r2evans. — Juan Riera, Feb 19 '23 at 18:53
I know of no function that automates "area between two curves" other than perhaps stefan's suggestion for `ggh4x::stat_difference` (I haven't tried it). Glad it works for you! — r2evans, Feb 19 '23 at 19:29

In ggplot, how to fill area between two normal curves

2 Answers2