In pharceutical industry, the changeover/cleaning events are typically very long and may even need different level of operator resource. As a result, they need to modelled carefully when we schedule the tasks and events. This is still something we can work with easily using CP-SAT solver.
But there is a concept called "Campaigning". It means we want continuously produce the orders of one product as much as possible. And there is a max number/limit for number of continuous production of the same product:
Suppose we have 10 orders for product A and the campaign size is 4. Then we typically do:
[A->A->A->A] -> changeover/cleaning -> [A->A->A->A] -> changeover/cleaning -> [A->A]
Of course, there shall always be changeover/cleaning between different products.
Suppose we have 1 order for product A and B respectively. Then we still have to do:
A -> changeover/cleaning -> B or B -> changeover/cleaning -> A
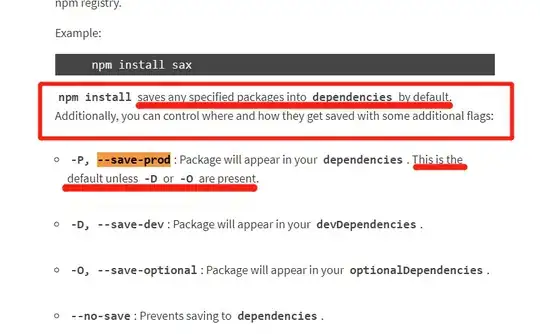
We did find a way to model this by creating Campaigns and optionally assign candidate Tasks into Campaigns and finally schedule the Campaigns instead. But the scalability of this solution is really bad. In the image below, when I have 5 orders for product A and B with limit being 2 orders, my laptop is already close to dead.
And the code is here: https://github.com/jiayi9/cp/blob/main/study_04_campaigning.py
We wonder is there any smarter way to tell the model how to do it.
The result using cumulative counting of tasks in a campaign and indicators of task reaching max size or not: https://github.com/jiayi9/cp/blob/main/example_24_campaigning_with_cumul.py