I'm implementing the Sieve of Eratosthenes, for an explanation of this see http://en.wikipedia.org/wiki/Sieve_of_Eratosthenes. However I would like to adapt it to generate M primes, not the primes 1 through N. My method of doing this is simply to create a large enough N such that all M primes are contained in this range. Does anyone have any good heuristics for modeling the growth of primes? In case you wish to post code snippets I am implementing this in Java and C++.
-
there is a version of the sieve algorithm you can implement with two arrays both with size equal to the count of primes you wish to find. One holds the primes, the other holds a prime multiple of the prime number at the same index. This way you don't need to compute the size of the sieve (N in your question). – hatchet - done with SOverflow Sep 26 '11 at 18:59
5 Answers
To generate M primes, you need to go up to about M log M. See Approximations for the nth prime number in this Wikipedia article about the Prime Number Theorem. To be on the safe side, you might want to overestimate -- say N = M (log M + 1).
Edited to add: As David Hammen points out, this overestimate is not always good enough. The Wikipedia article gives M (log M + log log M) as a safe upper bound for M >= 6.
- 16,761
- 4
- 37
- 72
-
1Re "*To be on the safe side, you might want to overestimate -- say N=M(log M + 1)*" -- That's not conservative enough. Example: The 1619th prime is 13693, but your expression only yields 13582.7. The wiki article does give an upper bound valid for all M>5, N = M log(M log M) – David Hammen Sep 26 '11 at 18:57
-
@David: Thank you for pointing that out! I have edited my answer. But I don't see your expression M log(M log M) in the linked article. – TonyK Sep 26 '11 at 19:20
-
1M log(M log M) = M log M + M log log M. This follows directly from from log(AB) = log A + log B and the distributivity of multiplication over addition. I don't know why the wiki article used the much more verbose right hand side of the identity. – David Hammen Sep 26 '11 at 19:44
-
If you don't trust my math, trust Wolfram Alpha's: http://www.wolframalpha.com/input/?i=M+log%28M+log+M%29+-+%28M+log+M+%2B+M+log%28log+M%29%29 . Scroll down to "*Alternate form assuming M is positive:*". – David Hammen Sep 26 '11 at 19:53
-
1@David: The only reason I didn't reply to your comment before last is that I was too embarrassed. Your logic is, of course, impeccable. – TonyK Sep 26 '11 at 20:14
-
also discussed here: http://stackoverflow.com/questions/1042902/most-elegant-way-to-generate-prime-numbers – hatchet - done with SOverflow Sep 27 '11 at 03:44
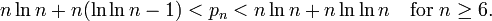
This approximation of the nth prime is taken from wikipedia; therefore you'll just need to allocate an array of m*log(m)+m*log(log(m)); an array of m*log(m) will be unsufficient.
- 2,261
- 2
- 19
- 27
Another alternative is a segmented sieve. Sieve the numbers to a million. Then the second million. Then the third. And so on. Stop when you have enough.
It's not hard to reset the sieve for the next segment. See my blog for details.
- 398,270
- 210
- 566
- 880
- 17,381
- 4
- 34
- 59
Why not grow the sieve dynamically? Whenever you need more primes, re-allocate the seive memory, and run the sieve algorithm, just over the new space, using the primes that you have previously found.
- 163,533
- 20
- 239
- 308
-
Plus this would defeat the point of the sieve, I would have to then reiterate over each of the previously discovered primes each time I grew the sieve, drastically slowing down my program. – daniel gratzer Sep 26 '11 at 23:27
-
right, that's what's known segmented sieve, I think. Just one clarification, you of course don't start anew from the beginning, but sieve ever increasing spans between the consecutive primes' squares, with each new prime (so no need to "**re-**allocate"). When there's not enough memory and you start using a shorter sieving array, @jozefg only then the performance will begin to suffer. – Will Ness Jan 28 '12 at 14:13
Lazy evaluation comes to mind (such as Haskell and other functional languages do it for you). Although you a writing in an imperative language, you can apply the concept I think.
Consider the operation of removing the remaining cardinal numbers from the candidate set. Without actually touching the real algorithm (and more importantly without guessing how many numbers you will create), execute this operation in a lazy manner (which you will have to implement, because you're in an imperative language), when and if you try to take the smallest remaining number.
- 32,434
- 14
- 99
- 159