The Weibull probability density function is given as such:
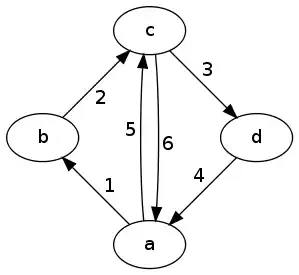
and the cumulative hazard function is represented as:
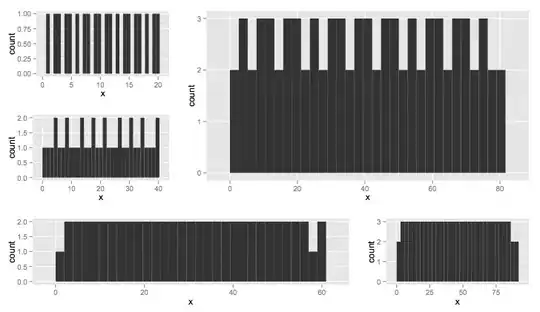
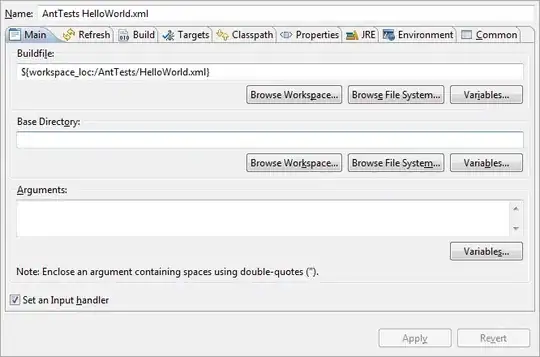
Now, I have a dataset where, the t and H are known as such:
## Import libraries
from scipy.optimize import curve_fit
from scipy import stats
from scipy.optimize import minimize
import numpy as np
import matplotlib.pyplot as plt
## Load the dataset
t = np.array([4, 6, 8, 10]) ## Time data
H = np.array([0.266919, 0.518181, 0.671102, 1.808351]) ## Cumulative Hazard
I wish to find the shape parameter(ρ) and scale parameter(λ) for the above dataset.
For simplicity of calculation, I have used the below logarithmic formulation:
Hence the logarithm for the time vector and Cumulative Hazard can be written as such:
ln_t = np.log(t) # log of time vector
ln_H = np.log(H) # log of Cumulative Hazard
I have applied below two methods
Method-1: By curve fitting using a linear function as such:
## Define a linear function
def ln_cum_hazard(LN_T, rho, myu):
LN_H = rho * LN_T - myu
return LN_H
## Model parameters
popt, pcov = curve_fit(ln_cum_hazard, ln_t, ln_H)
## Shape parameter
ρ = popt[0]
print("\n ρ (shape parameter) = \n", ρ)
## Scale parameter
λ = np.exp(popt[1]/popt[0])
print("\n λ (scale parameter) = \n", λ)
## Predicted values of H
H_pred = (t/λ)**ρ
## Plot H
plt.plot(t,H,'r',label = 'Actual Data')
plt.plot(t,H_pred,'b',label = 'Curve fit: scipy.optimize')
plt.legend()
plt.title('ρ = {} and λ = {}'.format(ρ,λ))
plt.xlabel('t')
plt.ylabel('H')
plt.show()
By curve fitting via scipy.optimize, I get the below fitted curve:
Method-2: By maximum likelihood estimation via stats.norm.logpdf()
## Define the linear function
def ln_cumulative_haz(params):
rho = params[0] # ρ (rho): Shape parameter
myu = params[1] # λ (lambda): Scale parameter
sd = params[2]
## Linear function
LN_H = rho * ln_t - myu
## Define the negative log likelihood function
LL = -np.sum( stats.norm.logpdf(ln_H, loc = LN_H, scale=sd ) )
return(LL)
## Inital parameters
initParams = [1, 1, 1]
## Minimize the negative log likelihood function
results = minimize(ln_cumulative_haz, initParams, method='Nelder-Mead')
## Model parameters
estParms = results.x
## Shape parameter
ρ = estParms[0]
print("\n ρ (shape parameter) = \n", ρ)
## Scale parameter
λ = np.exp(estParms[1]/estParms[0])
print("\n λ (scale parameter) = \n", λ)
## Predicted values of H
H_pred = (t/λ)**ρ
## Plot H
plt.plot(t,H,'r',label = 'Actual Data')
plt.plot(t,H_pred,'b',label = 'Curve fit: stats.norm.logpdf()')
plt.legend()
plt.title('ρ = {} and λ = {}'.format(ρ,λ))
plt.xlabel('t')
plt.ylabel('H')
plt.show()
By MLE via stats.norm.logpdf(), I get the below curve fit:
By both the methods, I have almost the same accuracy for ρ(shape parameter) and λ(scale parameter).
Now I have below 3 doubts:
Is the procedure to calculate the ρ and λ parameters correct for both the methods?
To define the negative log-likelihood function I have used "stats.norm.logpdf". However, the underlying function of data is a two parameter weibull distribution. Will this be correct?
Is there any other method to calculate the ρ and λ in Python?
Can somebody please help me out with these doubts?
Edit-1: Considering scipy.stats.weibull_min
I have applied below codes for minimization of negative log likelihood of weibull function.
## Define the linear function
def ln_cumulative_haz_weibull(params):
rho = params[0] # ρ (rho): Shape parameter
myu = params[1] # λ (lambda): Scale parameter
shape = params[2]
sd = params[3]
## Linear function
LN_H = rho * ln_t - myu
## Calculate negative log likelihood
LL = -np.sum( stats.weibull_min.logpdf(x = ln_H,
c = shape,
loc = LN_H,
scale = sd ) )
return(LL)
## Inital parameters
initParams = [1, 1, 1, 1] ## params[i]
## Results of MLE
results = minimize(ln_cumulative_haz_weibull, initParams, method='Nelder-Mead')
## Model parameters
estParms = results.x
ρ = estParms[0]
print("\n ρ (shape parameter) = \n", ρ)
λ = np.exp(estParms[1]/estParms[0])
print("\n λ (scale parameter) = \n", λ)
##ln_H_pred = estParms[0] * ln_t - estParms[1]
##print("\n ln_H_pred = \n",ln_H_pred)
H_pred = (t/λ)**ρ
print("\n H_pred = ",H_pred)
## Plot ln(H)
plt.plot(t,H,'r',label = 'Actual Data')
plt.plot(t,H_pred,'b',label = 'Curve fit: stats.weibull_min.logpdf')
plt.legend()
plt.title('ρ = {} and λ = {}'.format(ρ,λ))
plt.xlabel('t')
plt.ylabel('H')
plt.show()
However, the curve fitting results is not good by using stats.weibull_min.logpdf() and appear as such:
Also I get an error which states:
Warning (from warnings module): File "C:\Users\user\AppData\Local\Programs\Python\Python37\lib\site-packages\scipy\optimize\optimize.py", line 597 numpy.max(numpy.abs(fsim[0] - fsim[1:])) <= fatol): RuntimeWarning: invalid value encountered in subtract
Can somebody please help me out where am I going wrong?