I am attempting to use Seaborn to plot a bivariate (joint) KDE on a polar projection. There is no support for this in Seaborn, and no direct support for an angular (von Mises) KDE in Scipy.
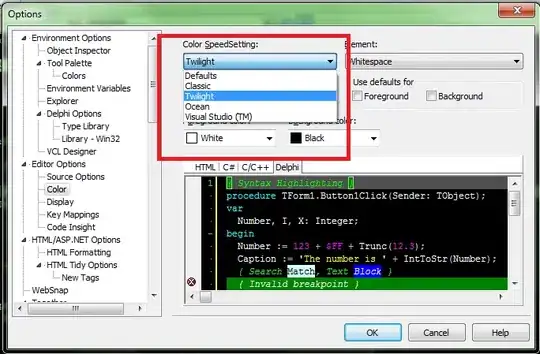
scipy gaussian_kde and circular data solves a related but different case. Similarities are - random variable is defined over linearly spaced angles on the unit circle; the KDE is plotted. Differences: I want to use Seaborn's joint kernel density estimate support to produce a contour plot of this kind -
but with no categorical ("species") variation, and on a polar projection. The marginal plots would be nice-to-have but are not important.
The rectilinear version of my situation would be
import matplotlib
import pandas as pd
from matplotlib import pyplot as plt
import numpy as np
import seaborn as sns
from numpy.random._generator import default_rng
angle = np.repeat(
np.deg2rad(
np.arange(0, 360, 10)
),
100,
)
rand = default_rng(seed=0)
data = pd.Series(
rand.normal(loc=50, scale=10, size=angle.size),
index=pd.Index(angle, name='angle'),
name='power',
)
matplotlib.use(backend='TkAgg')
joint = sns.JointGrid(
data.reset_index(),
x='angle', y='power'
)
joint.plot_joint(sns.kdeplot, bw_adjust=0.7, linewidths=1)
plt.show()
but this is shown in the wrong projection, and also there should be no decreasing contour lines between the angles of 0 and 360.
Of course, as Creating a circular density plot using matplotlib and seaborn explains, the naive approach of using the existing Gaussian KDE in a polar projection is not valid, and even if I wanted to I couldn't, because axisgrid.py hard-codes the subplot setup with no parameters:
f = plt.figure(figsize=(height, height))
gs = plt.GridSpec(ratio + 1, ratio + 1)
ax_joint = f.add_subplot(gs[1:, :-1])
ax_marg_x = f.add_subplot(gs[0, :-1], sharex=ax_joint)
ax_marg_y = f.add_subplot(gs[1:, -1], sharey=ax_joint)
I started in with a monkeypatching approach:
import scipy.stats._kde
import numpy as np
def von_mises_estimate(
points: np.ndarray,
values: np.ndarray,
xi: np.ndarray,
cho_cov: np.ndarray,
dtype: np.dtype,
real: int = 0
) -> np.ndarray:
"""
Mimics the signature of gaussian_kernel_estimate
https://github.com/scipy/scipy/blob/main/scipy/stats/_stats.pyx#L740
"""
# https://stackoverflow.com/a/44783738
# Will make this a parameter
kappa = 20
# I am unclear on how 'values' would be used here
class VonMisesKDE(scipy.stats._kde.gaussian_kde):
def __call__(self, points: np.ndarray) -> np.ndarray:
points = np.atleast_2d(points)
result = von_mises_estimate(
self.dataset.T,
self.weights[:, None],
points.T,
self.inv_cov,
points.dtype,
)
return result[:, 0]
import seaborn._statistics
seaborn._statistics.gaussian_kde = VonMisesKDE
and this does successfully get called in place of the default Gaussian function, but (1) it's incomplete, and (2) I'm not clear that it would be possible to convince the joint plot methods to use the new projection.
A very distorted and low-quality preview of what this would look like, via Gimp transformation:
though the radial axis would increase instead of decrease from the centre out.