If you were reading news about developments in graphics in the 1990s, you might have followed Jim Blinn's column in IEEE Computer Graphics & Applications, "Jim Blinn's corner." In the summer of 1997 you would have opened your issue to a column called "Floating-Point Tricks". All of the tricks are based on the following chestnut of knowledge Blinn passes along from Steve Gabriel and Gideon Yuval, two old hands at microsoft:
"If you only deal with positive numbers, the bit pattern of a floating point number, interpreted as an integer, gives a piecewise linear approximation to the logarithm function"
My question is, what is it about floating point numbers which gives rise to this characteristic?
Demonstration
// These are will result in undefined behavior
// and are not the 'right' way to do this
// but I am following Blinn 1997 here
int AsInteger(float f) {
return * ( int * ) &f;
}
float AsFloat(int i) {
return * ( float * ) &i;
}
// FISR demonstrating the logaritmic nature of the floating-point numbers
// The constant chosen is not "magic" but that which replaces the lost
// exponents from the shift of the number as an integer.
float BlinnISR(float x) {
int i;
float y;
// 0x5F400000 = 1598029824
// which is (AsInteger(1.0f) + (AsInteger(1.0f) >> 1))
i = 0x5F400000 - ( AsInteger(x) >> 1);
y = AsFloat(i);
// Blinn uses 1.47 and 0.47 not 1.5 and 0.5
// which are what you would get from differentiating
y = y * (1.47f - 0.47f * x * y * y);
return y;
}
The above, a recreation of Blinn's example code, shows how it works practically for the inverse square root.
Remember that 1 / sqrt(x) is the same as x(-1/2). So if we have access to a table of logarithms one way to find the square root is to take the natural log of x(-1/2) which gives you -1/2 * ln(x). If you exponentiate this you get 1 / sqrt(x) = e((-1/2) * ln(x)).
Right shifting the integer representation of the float bits gives us an approximation of a division by two of the logarithm of the input floating point number (this is our 1/2 * ln(x)). This is subtracted from the restoring constant, here just 0x5F400000, not yet 'magic' so we have essentially -1/2 * ln(x). Returning that to a float serves as our exponentiation step. We then have a number which serves as a good first input into Newton's method.
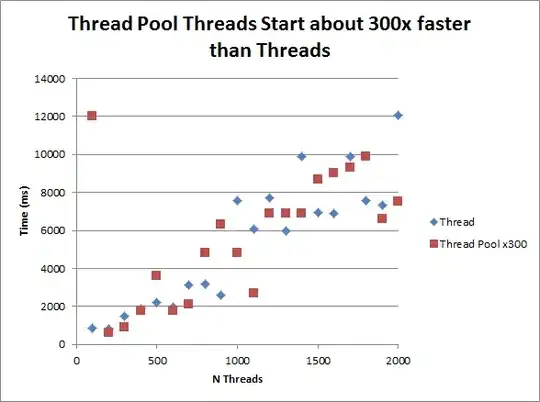
What it looks like
Visually, you can see the relationship here (Blinn 1997, p. 81):
A similar, idealized graph appears in Mitchell 1961 (p. 513, linked below):
This same relationship is shown in Jean-Michel Muller, ”Elementary Functions and Approximate Computing,” in Proceedings of the IEEE, vol. 108, no. 12, p. 2137, Dec. 2020
Where this applies
This characteristic is not unique to IEEE 754 floating point numbers, though that is where it is most famously exploited in Quake III Arena's fast inverse square root which uses a standard float. However it will work in an abstract format like Knuth's MIX didactic format, or with others, including the below examples.
To the best of my understanding, the relationship was first recorded in the academic press with John Mitchell's 1961 Computer Multiplication and Division Using Binary Logarithms demonstrating the method with an abstract binary logarithm system. William Kahan implemented a similar scheme around 1961 or 1962 on an IBM 7090. We know as well, in part due to Noah Hellman's masters thesis, Mitchell-Based Approximate Operations on Floating-Point Numbers, that it was also implemented in UNIX as the system square root from 1974 until the creation of a libm for BSD 4.3 in the mid 1980s. Around that same time, Kahan and his graduate student K-C Ng produced but did not publish a 'magic' square root using this method designed to operate on not floats but doubles which would be halved and operated on as 32 bit parts (see a related stackoverflow question).
It will not, however, work for all floating point formats. DEC's VAX floating point format interleaves the sign, exponent and fraction portion (which it splits into two) so it won't do.
What I am not asking
I don't care (for this question) about how engineers came to learn about this relationship, or where it has been exploited (cf the FISR). I want to know why it exists. Historical questions I've asked which sort of relate to the topic would be found on the retrocomputing stack exchange: early examples of indexing float bits in C, type punning and C standards/compilers
I'm also not asking how to do it, though a good answer might include an illustrative example with some code. However, you should first take a look at this amazing FISR question on codegolf to see some really interesting ones.
An excellent answer
A bad answer might be "any working engineer with a slide rule would understand this relationship," though I could imagine that a great answer might resort to a slide rule. Another bad answer might be "because Knuth says so," while a very good answer might include that sentiment amidst an explanation which depends on section 4.2.4 of Volume 2 of TAOCP (I don't have page numbers, I have O'Reilly's pagination abomination, it is pp. 240-247 in the print first edition).
An excellent answer should provide a clear understanding of the nature of the relationship and why it arises. A proof that the relationship must be so would be intruiging, though I can forsee some challenges.
Why I am asking
I am writing a history of the Fast Inverse Square Root, information about which is collected at 0x5f37642f.com. Part of investigating this as a historian means asking questions like this from the community. I do not have the expertise to distill, by myself, much of this because I am not a mathematician or a computer scientist.
The FISR has basically three interesting parts: the logarimic approximation, the "magic" constant", and newton's method. Between the three when folks write about the FISR they write about the magic constant, then newton's method, then spend very little time talking about the approximation. I get the feeling from the broader 'literature' that the approximation is widely known but not as clearly well understood. What I learn from answers will help me understand it.
An excellent answer will be noted in the acknowledgements of papers or talks which come out of this work.
I'm also asking because c'mon, no one has asked this yet and we've been here HOW long?