How to interpolate logarithmically evenly-spaced data using scipy.interpolate.interp1d?

Question

I have a real-valued function G(t) which I want to interpolate over logarithmically evenly-spaced times: 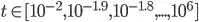. This is needed in order to obtain an approximate expression of the components of G as a function of the frequency 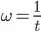instead of the time. I thus defined a times list this way:

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d

exponents = np.linspace(-2, 6, 81, endpoint=True) #81 values
ts = [10**(xp) for xp in exponents] #times (s)

I used numpy.linspace there as numpy.logspace seemed to be generating errors. The end result should look somewhat like this (the different-colored curves are each obtained depending on another parameter which is not relevant here):

To do so, I tried to use scipy.interpolate.interp1d as can be seen in the function below:

def G_pr_sec(ts, Goft):
    """
    Returns G_prime and G_sec at frequencies 1/ts[i] by interpolating the array Goft

    Parameters
    ----------
    ts : 1D array
        Array of times
    Goft : 1D array
        Values of G(t)
        
    Returns
    -------
    G_pr : 1D array
        Array of G_prime(1/t)
    G_sec : 1D array
        Array of G_second(1/t)

    """
    G2 = interp1d(ts, Goft)
    
    G_pr = []
    G_sec = []
    
    for t in ts:
        res_sec = 0
        res_sec += -0.47*(G2(2*t) - G2(4*t)) + 1.674*(G2(t) - G2(2*t)) + 0.198*(G2(t/2) - G2(t))
        res_sec += 0.62*(G2(t/4) - G2(t/2)) + 0.012*(G2(t/8) - G2(t/4)) + 0.172*(G2(t/16) - G2(t/8))
        res_sec += 0.0433*(G2(t/64) - G2(t/32)) + 0.0108*(G2(t/256) - G2(t/128))
        res_sec += (0.0108/4)*(G2(t/1024) - G2(t/512)) + (0.0108/16)*(G2(t/4096) - G2(t/2048))
        res_sec += (0.0108/64)*(G2(t/(64*256)) - G2(t/(32*256))) + (0.0108/256)*(G2(t/(256**2)) - G2(t/(128*256)))
        G_sec.append(res_sec)
        
        res_pr = 0
        res_pr += G2(t) -0.142*(G2(4*t) - G2(8*t)) + 0.717*(G2(2*t) - G2(4*t)) + 0.046*(G2(t) - G2(2*t))
        res_pr += 0.099*(G2(t/2) - G2(t)) + 0.103*(G2(t/4) - G2(t/2)) + 0.001*(G2(t/8) - G2(t/4))
        res_pr += 0.00716*(G2(t/16) - G2(t/8)) + 0.000451*(G2(t/64) - G2(t/32))
        G_pr.append(res_pr)
        
    return [G_pr, G_sec]

But immediately got the following error when calling G_pr_sec(ts, Gs) with Gs containing the values of the function G(t) for all times in ts, G(t) being a real-valued function defined above in the file (its exact definition is not important there, I believe):

ValueError: A value in x_new is below the interpolation range.

After a quick research, it seems that this error occurs whenever the data passed in x (or in the present case t) is not linearly evenly-spaced, so nothing unusual yet.

However, when I tried to apply the method specified there by defining a function log_interp1d the following way:

import scipy as sp
import scipy.interpolate

def log_interp1d(xx, yy, kind='linear'):
    logx = np.log10(xx)
    logy = np.log10(yy)
    lin_interp = sp.interpolate.interp1d(logx, logy, kind=kind)
    log_interp = lambda zz: np.power(10.0, lin_interp(np.log10(zz)))
    return log_interp

And replacing interp1d by log_interp1d in the body of the previous function, the exact same error occured, which confuses me quite a lot.

I have looked up other links, but none seemed to provide reliable advice in order to tackle this problem. I could still use linearly evenly-spaced times to do this interpolation, but this would result in a very uneven spacing of the data once in log-scale and I want to avoid this. How could I interpolate my data while keeping logarithmically evenly-spaced time (and thus frequency) values ?

Thanks in advance !

Answer 1

The error is not related to log or other data spacing. It's just what it says on the tin: you are trying to evaluate the interpilator outside of the interpolation range (x.min(), x.max()).

To avoid the error, pass bounds_error=False to interp1d. However the quality of extrapolation can vary wildly, so YMMV. I'd suggest to reevaluate the approach and figure out why you are extrapolating and if you can use some outside knowledge instead.