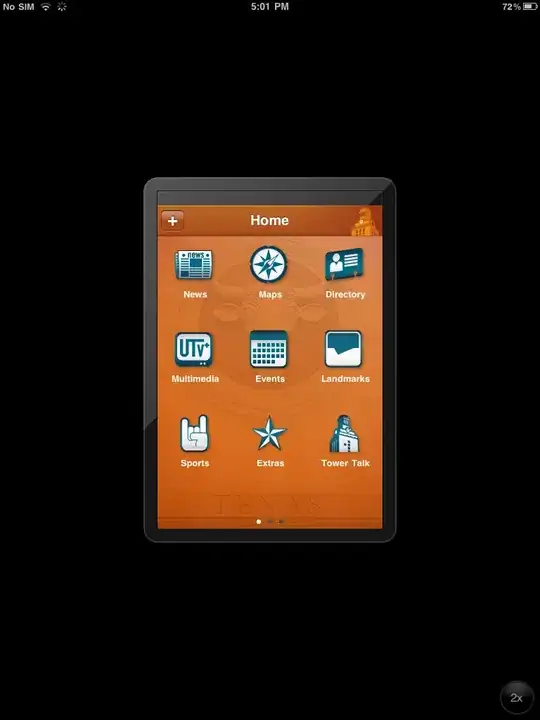
I have the following point configuration:
import numpy as np
T=np.array([9,9])
X1=np.array([8,16])
X2=np.array([16,3])
points=np.array([[4, 15],
[13,17],
[2, 5],
[16,8]])
This can be represented as:
Given T, X1, and X2, I want to find all points of the array points that are inside the yellow region. This yellow region is always in the "opposite side" of the points X1 and X2.
How can I achieve this in a simple and efficient way?
Edit1 (trying B Remmelzwaal solution)
T=np.array([9,9])
X1=np.array([10,2])
X2=np.array([2,15])
points=np.array([[2, 5]])
valid_points = list()
# calculating y = mx + b for line T, X1
slope1 = np.diff(list(zip(T, X1)))
m1 = np.divide(slope1[1], slope1[0])
b1 = T[1] - m1*T[0]
# calculating y = mx + b for line T, X2
slope2 = np.diff(list(zip(T, X2)))
m2 = np.divide(slope2[1], slope2[0])
b2 = T[1] - m2*T[0]
for point in points:
# check if point is under both lines
for m, b in (m1, b1), (m2, b2):
if point[1] > m*point[0] + b:
break
else:
# only append if both checks pass
valid_points.append(point)
print(valid_points)
The configuration is the following:
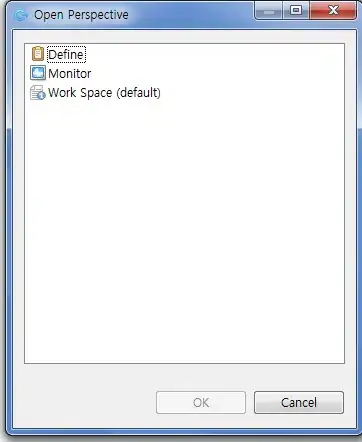 and the code returns returns
and the code returns returns [2,5] and it should return []. This is not correct since the region of interest is now in the opposite region (see image)