5

I trying to make a dynamic Excel formula that sums values in a row when the values in another row are 1 followed by 0. If after the last 0, there is a 1, the sum again until you reach another 1. enter image description here

As you can see in the picture, the first value in the F6 must be 323 (202+47+74), then a 1 appears but no 0 below, so the value remains the same (1997). Then another 1 followed by two 0 that makes 9 (4+3+2), and so on.

Joaquin Osses
  • 71
  • 3

6 Answers6

5

Here is another alternative,

enter image description here

• Formula used in cell F2

=LET(
a,B2:B13,
b,C2:C13,
c,SCAN(0,a,LAMBDA(x,y,x+y)),
d,UNIQUE(c),
IF(a=0,"",INDEX(MMULT(N(TOROW(c)=d),b),XMATCH(c,d))))

Notes: Refer below what each variable does:

• Firstly, we are taking both the ranges i.e. B2:B13 & C2:C13 and defining them as a & b respectively.

• Next, we are using SCAN() function to return an array, with an initial value of 0 it iterates over each value in the sequence of a which adds the current x to the accumulated value of y from the previous iterations using the LAMBDA(). The return is assigned as c.

enter image description here

SCAN(0,a,LAMBDA(x,y,x+y))

• Now, we are using UNIQUE() function to remove any duplicates from c

enter image description here

=LET(
a,B2:B13,
b,C2:C13,
c,SCAN(0,a,LAMBDA(x,y,x+y)),
d,UNIQUE(c),
d)

• Next, we are performing a matrix multiplication using the MMULT().

N(TOROW(c)=d)

The above compares each value in the array c with each in the array d and returns a BOOLEAN array of the same size where if its equal then TRUE else FALSE. Then the MMULT() performs the matrix multiplication which results in same numbers of rows and columns as in b where it sums the product of each value of BOOLEAN with corresponding b.

MMULT(N(TOROW(c)=d),b)

enter image description here

• Finally we are using an IF() and INDEX() wtih XMATCH() to return the required output as desired.

enter image description here

==> The XMATCH() function is used to find the position of each value of c within the array d which is used within the INDEX() to return the corresponding values of the above matrix multiplication. Lastly wrapping it within the IF() function which checks if any value in the array a is equal to 0 then it returns empty else it gives the value returned using INDEX() & XMATCH().

Ofcourse, you don't have to fill down, as it will spill dynamically.

Mayukh Bhattacharya
  • 12,541
  • 5
  • 21
  • 32
  • 2
    Good use of `MMULT`. I personally would prefer slightly smaller screenshots - at that size they tend to detract a bit from your otherwise very good answer. – Jos Woolley Jun 08 '23 at 07:49
  • Thank you so much @JosWoolley Sir =) It means a lot. Thanks again, you have no idea, how much it means when those words comes from `Experts` like you. I will try to follow as you have suggested about the screenshots. – Mayukh Bhattacharya Jun 08 '23 at 07:50
  • 2
    FYI @MayukhBhattacharya I did some performance tests (check my answer) and your solution has the best performance in the three scenarios I tested. Just a comment `d` in your formula is in ascending order, so you can optimize the search in `XMATCH` using `search_mode` input argument and set it to `2`, so you can have: `XMATCH(c,d,,2)`. Great solution! – David Leal Jun 09 '23 at 22:01
4

This could also be done without helpers/lambda using MMULT:

=LET(a, B3:B14,
     b, C3:C14,
     x, SEQUENCE(ROWS(a)+1),
     y, DROP(MMULT(--(TOROW(x)<=x),--VSTACK(a,1)),-1),
IF(a,MMULT(--(TOROW(y)=y),b),""))

It first stores ranges a and b for easy reference in the formula.

Then x is a counter of the number of rows of range a +1 *. x is used in y to check if x is equal to or greater than other values in the range multiplied by the qty of 1 found in these rows from range a*.

* An extra 1 is added to the range a in order to simulate a final 1 in the range a up to where we want to sum the final values evetually.

So y is a counter that starts at the first found 1 and adds up +1 if value in a equals 1 again. After having calculated this the helper row at the end is no longer needed, since it calculated up to where it should sum. Therefore we remove (drop) the last row from y for size compatibility to the range to sum (b).

Finally it checks if a is 1. If it does it sums the rows of b where the rows in y equal the number in that row of y.

enter image description here

P.b
  • 8,293
  • 2
  • 10
  • 25
  • 1
    King of `MMULT()` i would say everytime. =) – Mayukh Bhattacharya Jun 08 '23 at 07:51
  • 1
    MMULT is very powerful. I learned it on here. I think this post of MarkFitzpatrick got me looking into what it does: https://stackoverflow.com/a/68594673/12634230 – P.b Jun 08 '23 at 08:18
  • Checking that now, right away. Yes its very powerful indeed. – Mayukh Bhattacharya Jun 08 '23 at 08:20
  • Interesting application of `MMULT` @P.b, the only comment I have is that second `MMULT` call repeats the same calculation for `0` values within the same group, which is some kind of overhead. I had the same problem with my first approach. Similar with Mayukh's solution, that is why it needs `UNIQUE`. Other than that it is a great solution on how to get the same result without `LAMBDA` helper functions. – David Leal Jun 08 '23 at 13:28
  • 3
    Nice. You could always make a nice condense hybrid `=LET(a,B3:B14,y,SCAN(0,a,LAMBDA(q,r,q+r)),IF(a,MMULT(N(TOROW(y)=y),C3:C14),""))` – JvdV Jun 08 '23 at 15:05
  • @JvdV nice and short – P.b Jun 08 '23 at 16:03
  • 2
    @DavidLeal if the range is large it's worth storing the unique values and using that in the calculation. I chose not to for keeping the formula more understandable. – P.b Jun 08 '23 at 16:08
  • @DavidLeal actually the second Mmult doesn't refer to 0's it refers to the cumulative counter (results similar like in second screenshot of Mayukh's answer). Just replace the final Mmult with `y` to see what it does. – P.b Jun 08 '23 at 18:36
  • when I reviewed it, what I saw that the `MMULT` calculation is repeated, I thought it refers to the row positions where are the zeros in column `B` from your screenshot, i.e. the same cumulative sum within each group. I referred to this portion of the formula: `MMULT(--(TOROW(y)=y),b)`. The result is repeated for the zero values, so it made me think that this calculation is done multiple times within all the zeros within the same group returning the same value. This is what I meant as overhead calculation, but maybe I am wrong. – David Leal Jun 08 '23 at 18:45
  • It has a function. If the value in `a` is 0 it gives `""` instead of the MMULT. Since `a` is either `1` or `0` I had IF interpret it as boolean – P.b Jun 08 '23 at 19:04
  • yes, but `MMULT` doesn't depend on `a` so once it is `TRUE` it returns the calculation of `MMULT`, that is done only once, but the same calculation is carried out for all rows with `0` within the same group. Therefore for the first `1` it calculates three times `323` but it needs only the first one. For a large number of zeros within the same group, it might by significant overhead, but maybe it is not relevant compared to other approaches, something to test for curiosity. – David Leal Jun 08 '23 at 19:23
  • How about: `=LET(a, B3:B14, b, C3:C14, x, SEQUENCE(ROWS(a)+1), y, DROP(MMULT(--(TOROW(x)<=UNIQUE(x)),--VSTACK(a,1)),-1),m,MMULT(--(TOROW(y)=UNIQUE(y)),b),IFERROR(1/a*INDEX(m,y),""))` – P.b Jun 08 '23 at 19:49
  • 1
    @P.b for example I tested my solution using `XLOOKUP` (formula 2) and your initial solution for `1000` rows with the worse case scenario `1` on the first row and the rest zeros. My solution took `0ms` and your solution `160ms` on average for example. – David Leal Jun 08 '23 at 19:52
  • And my comment above? – P.b Jun 08 '23 at 19:53
  • 1
    @P.b better under this new approach from your comment, around `80ms` for `1000` rows – David Leal Jun 08 '23 at 19:58
  • @P.b I don't know why but around 7350 rows, I am getting `0` as result for your second solution. – David Leal Jun 08 '23 at 20:13
  • Let us [continue this discussion in chat](https://chat.stackoverflow.com/rooms/254005/discussion-between-p-b-and-david-leal). – P.b Jun 08 '23 at 20:44
3

Sum Up Groups

enter image description here

=LET(o,B3:B14,v,C3:C14,c,1,n,"",
    r,ROWS(o),rs,SEQUENCE(r),iss,FILTER(rs,o=c,""),
    ies,IF(ROWS(iss)=1,r,VSTACK(DROP(iss-1,1),r)),
MAP(rs,LAMBDA(mr,
    IF(INDEX(o,mr)<>c,n,LET(
        ri,XMATCH(mr,iss),is,INDEX(iss,ri,1),
        ie,INDEX(ies,ri,1),sr,SEQUENCE(ie-is+1,,is),
    SUM(INDEX(v,sr)))))))
VBasic2008
  • 44,888
  • 5
  • 17
  • 28
  • 2
    quick note, for the following scenario: 1 on the first row and zeros for the rest of them, the formula produces an error. In such case, probably you need to consider it in the definition of `ies` – David Leal Jun 09 '23 at 02:28
  • 1
    @DavidLeal Nice catch, thanks. It is hell to fix an already inferior solution (see the other answers). It looks like a simple fix but it took quite a while since I first encountered a few surprises after going with `If(iss="","",...`. I hope the ideas are sound at least. – VBasic2008 Jun 09 '23 at 07:05
  • 2
    thanks, I guess I found a quick fix, replacing: `VSTACK(DROP(iss-1,1),r))` with `IFERROR(VSTACK(DROP(iss-1,1),r),r)`. I found the error trying to do some performance tests with your solution. I am not sure about your statement about the quality of your solution. Other solutions are shorter, but it doesn't mean they perform better. I have found that solution using `MMULT` reaches some limit around `7500` rows and some performance issues for this worse case scenario. I am checking it with @P.b – David Leal Jun 09 '23 at 13:17
  • 2
    I tested your solution for this worse case scenario: `1` in first row and the rest of the rows `0` and it performs as good as mine solution (*formula 2*) around `20ms` for `7000` rows and it also works for more than `7500` rows, limit I found for P.b solution for example. My hypothesis is that such solutions using `MMULT` perform worse when within groups there are a large number of zeros, that is why I am testing this scenario. – David Leal Jun 09 '23 at 13:23
  • 2
    For a random scenario generating `0`s and `1`s for for `7000` rows, your solution takes around `1,120ms` which is `8x` time faster than my solution using `XLOOKUP` and P.b solution even for the corrected solution provided in the comment section of his answer. – David Leal Jun 09 '23 at 13:29
  • 2
    @DavidLeal Thanks for the valuable info and the boost of moral. – VBasic2008 Jun 10 '23 at 05:10
3

Here another array solution approach, i.e. it spills the entire result all at once (formula 1):

=LET(A,A1:A12, B,B1:B12, n,ROWS(A), seq,SEQUENCE(n),
 MAP(seq, LAMBDA(s,IF(INDEX(A,s)=1,LET(end, @FILTER(seq, (seq>s) * (A=1),n+1),
 SUM(FILTER(B, (seq>=s) * (seq<end)))),""))))

or you can use this alternative (formula 2). The previous formula has a little overhead calculation, because we need to get just the first element of the first FILTER call, but we get the entire FILTER output. The following formula avoids that.

=LET(A,A1:A12, B,B1:B12, n,ROWS(A), seq,SEQUENCE(n), idx,IF(A=1,seq,0),
 MAP(idx, LAMBDA(x, IF(x=0,"", SUM(FILTER(B, (seq>=x) 
  * (seq<XLOOKUP(x+1,idx,idx,n+1,1))))))))

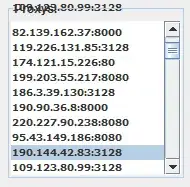
Here is the output for formula 1: output

In formula 1 it iterates via MAP over all index positions of the input (seq). On each iteration (s) it checks for the given index s if the column A values (A) is equal to 1 via INDEX. If that is the case (otherwise it returns an empty string), it finds the index position (end) of the next 1 value for index position greater than the current iteration value (s) via FILTER function. Since we are only interested in the first value (index position of the next 1 value) of the FILTER output we use Implicit intersection operator: @. If the condition doesn't match, then we use the third input argument of FILTER to return n+1, where n is the number of rows of the input data.

Since end represents the index position of the next 1 value or the number of rows plus one in case no more 1 value were found, now we can use FILTER again to select B column values (B) from s to end-1 index positions and sum it.

In formula 2 it identifies first the index positions where A is equal to 1 (idx), otherwise returns 0. By definition non zero values of idx are in ascending order. To identify the end of the interval (position of the following 1 value in A), it uses XLOOKUP with approximate search (1-equal or greater) to look for the next element of x, i.e. x+1. It returns the position of the next 1 value in A, otherwise the n+1. Therefore the range of the B to sum is filtered for the index positions seq between x and the output of XLOOKUP.

Performance Analysis

Here a summary based on different scenarios to measure the performance of different answers provided to this question. I am considering the following scenarios:

  1. A: worse case scenario, 1 in the first row and the rest with zeros
  2. B: Random set for column A, with significant more 0s than 1s
  3. C: Random set for column A, with uniform distribution for 1s and 0s.

In all cases I am considering an input of 7000 rows.

To generate a non-uniform [0,1]-distribution I use the following:

=LET(rnd, RANDARRAY(10000,1,1,10,1),IF(rnd=1,1,0))

I am considering the following solutions:

  1. Provided by: @VBasic2008 with the correction indicated in the comment section of his answer.
  2. Provided by: @MayukhBhattacharya. This solution uses MMULT, but it works for more than 7500 rows.
  3. Provided by: @P.b (initial approach, not the approach provided in the comment section, which doesn't provide a correct result). Worth to notice that this solution stops working around 7500 rows.
  4. Provided by @DavidLeal formula 2 using XLOOKUP. The formula 1 was inefficient, so it was not considered in the analysis.

Here are the results for Excel Desktop:

Scenario MayukhBhattacharya VBasic2008 DavidLeal P.b
A 10ms 1,070ms 10ms 7,300ms
B 560ms 1,310ms 970ms 7,710ms
C 2,640ms 2,270ms 4,780ms 7,590ms

I would say the solution provided by @MayukhBhattacharya is the best one in all scenarios tested, then the solution provided by @VBasic2008, it works pretty well, but it fails for the worse case scenario (A) taking significant time.

It brought my attention that running the same test under Excel for Web (free version). I don't get the same results. Again MayukhBhattacharya and VBasic2008 are the best solutions, but this time the solution provided by VBasic2008 performs better:

Scenario MayukhBhattacharya VBasic2008 DavidLeal P.b
A 0ms 0ms 10ms 9,950ms
B 770ms 40ms 1,570ms 10,080ms
C 3,640ms 850ms 9,930ms 10,440ms

I tested also @JvdV, provided in the comment section of P.b solution, which is at the end a variation of @MayukhBhattacharya approach. @JvdV is more efficient than @P.b solution, but worse than @MayukhBhattacharya solution.

Worth to mention that @MayukhBhattacharya solution can be optimized because the input argument lookup_array from XMATCH is sorted in ascending order, so we can use a binary search in XMATCH using the input argument search_mode=2. Which provides an improvement around 9%. The same optimization applies to @VBasic2008 solution, since it uses XMATCH with lookup_array in ascending order.

Here is the link to the Excel file used for doing the performance analysis. The summary of the result is on the first tab. Be aware the file has the following configuration: Formulas -> Calculation Options->Manual, to avoid any specific calculation interfere other results. It uses volatile Excel functions (RANDARRAY, NOW) so it avoids automatic recalculation.

It would be interesting to verify the results by others.

Conclusion

Using the idea of finding start/end for each group, used by @VBasic2008 and by @DavidLeal. Using INDEX performs better than FILTER. For example @DavidLeal solution modified to remove FILTER as follows has a similar performance as @VBasic2008 solution, but not better:

= LET(A,A1:A12, B,B1:B12, n,ROWS(A), seq,SEQUENCE(n), idx, 
  IF(A=1,seq,0), MAP(idx, LAMBDA(x, IF(x=0,"",
  LET(xe, XLOOKUP(x+1,idx,idx,n+1,1)-1,SUM(INDEX(B, SEQUENCE(xe-x+1,,x))))))))

@VBasic2008 solution has a simple way to find start/end of the intervals, compared to the previous formula, therefore the performance is better.

Solutions using MMULT to identify each group, work better when the calculation involves a reduced portion such as in @MayukhBhattacharya solution, compared to @P.b solution. Which is also good to avoid any possible Excel limits.

Both approaches are good strategy, taking into account previous considerations.

Still an open question, why some scenarios work better depending on Excel platform (Desktop, Web) used. Probably internally the functions are not implemented in the same way, or different version for the same functions used.

David Leal
  • 6,373
  • 4
  • 29
  • 56
1

You can do this easily with a (hidden) extra column. Keep the running total in the hidden column, and display that running total only when the [0, 1] column is 1.

Please note, in future posts provide the data as a table we can copy, not as a screenshot.

Matching the rows in your data, in row 3 in the hidden column (F is the hidden column here):

=IF(B3=1, IF(B4 = 1, C3, D4+C3), IF(B4 = 1, C3, C3+D4))

Copy that down column F.

In row 3 in the display column (G here):

=IF(B3 = 1, F3, "")

Of course, copy that down column G.

  A B C G
1        
2        
3   1 202 323
4   0 47  
5   0 74  
6   1 1997 1997
7   1 4 9
8   0 3  
9   0 2  
10   1 2 2
11   1 5 5
12   1 1981 1981
13   1 3 11
14   0 8  
RichardCook
  • 846
  • 2
  • 10
  • 1
    If you are using a newer version of excel then using ifs might be more efficient and easier to read than nested if statements – JoeJam Jun 07 '23 at 23:21
  • @JoeJam is right. I'm stuck with Excel 2019. I've been wondering if 365 offers dynamic formulas that would make this easier. If so, go that route. – RichardCook Jun 07 '23 at 23:36
  • @JoeJam I've been hoping you'd offer us a more efficient approach. Posting an improved solution is more useful than saying there might be one. – RichardCook Jun 08 '23 at 00:27
  • 1
    you have inspired me to write my own answer! – JoeJam Jun 08 '23 at 20:22
1

A simpler answer than many others are suggesting is as follows (inspired by @richardcook)
Have a helper column for when there are multiple zeroes in column B:

enter image description here The formula for the helper column is =IF(AND(C4=0,C5=0),D4+F5,D4) and the formula for the final answer is =IFS(C4=0,,AND(C4=1,C5=1),D4,AND(C4=1,C5=0),D4+F5)

What the block of ifs is doing is similar to RichardCook's answer where the formula checks to see if the initial column is 1 or 0 and if the column is 1 checks to see if there are multiple zeroes. If there are multiple zeroes it uses the helper column to find the total.

JoeJam
  • 371
  • 1
  • 14