X Y
-------
1 1
2 1
3 3
4 1
5 3
6 5
7 7
8 1
9 3
10 5
11 7
12 9
13 11
14 13
15 15
16 1
17 3
18 5
19 7
20 9
21 11
22 13
23 15
24 17
25 19
26 21
27 23
28 25
29 27
30 29
31 31
32 1
33 3
34 5
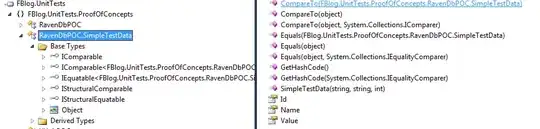
I tried representing the pattern in form of line graph.
The pattern is like this,
if n is of the form 2^N then f(n) = 1 else f(n) = f(n-1)+2
Also, use f(1) = 1 as base condition (already covered by above logic)