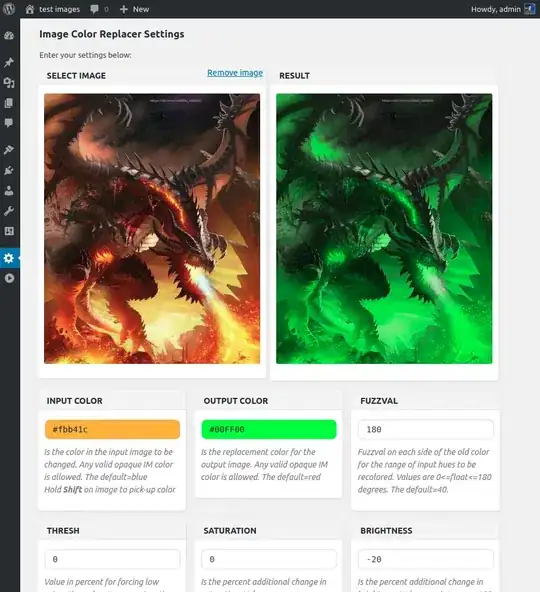
I was watching youtube video of implementing Binary Search Tree and this is the function where I can get the maximum height of tree.
int MaxHeight(BstNode* root) {
if (root == NULL) {
return -1;
}
return max(MaxHeight(root->left),MaxHeight(root->right))+1;
}
I roughly get how this function get the height but not exactly. I wonder how this function flows....
I thought as soon as the function gets to the end of the node it return -1 and it is incrementing to the root by 1?