0

I am using the Python library function scipy.minimize to solve a series of linear equations with constraints, maximising the radius of a circle inscribed inside a polygon. See here for a visualization of what a circle inscribed inside a polygon is:

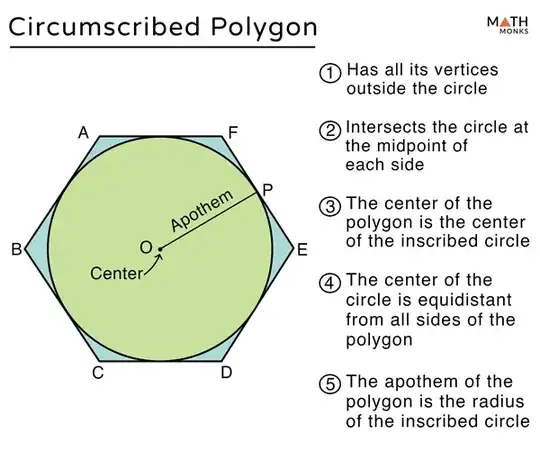
inscription

The constraints of the optimisation are the following: the distance between circle middlepoint with the coordinates (x[1],x[2) and every single line of the polygon has to be bigger than the radius - otherwise the circle radius would reach outside the polygon and the circle would no longer be inscribed.

These constraints are formulated through the following lambda functions, one function for each side of the polygon (a triangle, in our example):

# all of these functions have to remain non-negative
constraint1 = lambda x: distance_to_line((x[1],x[2]),polygon_points[0],polygon_points[1]) - x[0]
constraint2 = lambda x: distance_to_line((x[1],x[2]),polygon_points[1],polygon_points[2]) - x[0]
constraint3 = lambda x: distance_to_line((x[1],x[2]),polygon_points[2],polygon_points[3]) - x[0]

The variables here are x[0] for the circle radius and x[1], x[2] for the coordinates of the circle middlepoint.

variables = [0, 0, 0]

The objective function is the opposite of x[0], which is the circle radius:

def objective (x):
    return -(x[0])

Feeding these components into the minimise function gives correct results, the program works like this and result.x[0] prints the correct radius:

constraints = [{'type': 'ineq', 'fun': constraint1},{'type': 'ineq', 'fun': constraint2},{'type': 'ineq', 'fun': constraint3}]

result = minimize(objective, variables, constraints=constraints)

print("Maximum radius: " + str(result.x[0]))

So far, so good. But this is where a problem arises. As you might have noticed, it makes sense to generate the constraint functions through list comprehension, so a potentially infinite number of polygon lines can be processed.

all_constraints = [lambda x: distance_to_line((x[1],x[2]),polygon_points[i],polygon_points[i+1]) -x[0] for i in range (0,3)]

But scipy.minimize no longer works if I feed it these three list comprehension-generated lambda functions instead of the manually written ones:

constraints = []
for function in all_constraints :
    constraints.append({'type': 'ineq', 'fun': function})

Instead, I get various error messages in result.message like "Singular matrix E in LSQ subproblem" or "Inequality constraints incompatible".

This confuses me greatly, because the functions generated by list comprehension and those written manually at the start should be completely equivalent in content and results.

Are all_constraints really equivalent to the three manually written functions above, or am I making a mistake somewhere?

Reinderien
  • 11,755
  • 5
  • 49
  • 77
Desenchantee
  • 13
  • 4
  • Your equations cannot be linear, because `distance_to_line` cannot be linear, right? – Reinderien Jul 05 '23 at 15:05
  • The program works fine with the manually written functions, so the distance_to_line method doesn't seem to be the issue. – Desenchantee Jul 05 '23 at 15:17
  • Whether it's the main issue or not, it's important to get your terminology right. If this is actually linear, then this is an x/y problem and you shouldn't be using `minimize` at all – Reinderien Jul 05 '23 at 15:19
  • 1
    Python's `lambda`s are *late-binding closures*. See, for example, https://stackoverflow.com/questions/37791680/scipy-optimize-minimize-slsqp-with-linear-constraints-fails/37792650#37792650 for an answer to a similar question. – Warren Weckesser Jul 05 '23 at 16:53

1 Answers1

1

You are running into a problem very well described here: https://stackoverflow.com/a/34021333/22174676

The TL;DR is: the lambda functions will refer to the variable I when they are called, instead of using the value of i when the lambda is defined. Because of this when you run the constraints, it will use the last value of i for all constraints, which will result in all constraints being the same and the system non-solvable.

To partially define each function according to the i variable consider defining a general constraint function that depends on x and i, and using partial (from functools) to create all constraints, like this:

from functools import partial
def const(x, i):
    return distance_to_line((x[1],x[2]),polygon_points[i],polygon_points[i+1])-x[0]

all_constraints = [partial(const, i=i) for i in range(3)]
Lourenço Monteiro Rodrigues
  • 26
  • 3
  • Thanks, that seems to describe my problem very well. As for whether your solution worked out, I'll give feedback once I tried it out. – Desenchantee Jul 05 '23 at 15:17