Plotting imaginary numbers on a complex plane

Question

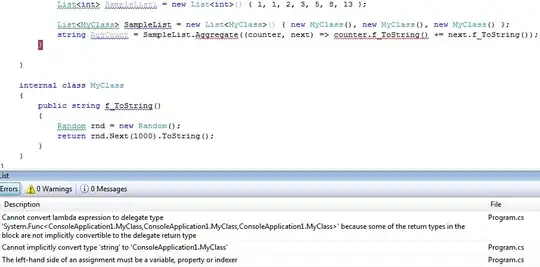
I'm trying to plot the graph of Euler's formula (e^(ix)) on a complex plane (preferably with matplotlib) to achieve the circular graph (radius i). Is there a way I can do this?

So far I've only managed to plot it on a real plane to get a graph in the form e^(kx) with the following code:

import numpy as np
import matplotlib.pyplot as plt

i = np.emath.sqrt(-1).imag
e = math.e

x = np.linspace(0, 10, 1000)
plt.scatter(x, (e**(i*x)))
# plt.scatter(x, (np.cos(x) + (i*np.sin(x))))
plt.show()

Just compute the complex valued function for some values of x and then plot x= and y=. Don't mix up the variable you're naming x and the x-axis on the plot. — Brian61354270, Jul 13 '23 at 20:10
Also, note that `np.emath.sqrt(-1).imag` can just be written as `1j`. Python has complex literals built in — Brian61354270, Jul 13 '23 at 20:10

score 4 · Accepted Answer · edited Jul 13 '23 at 20:49

You can compute the complex-valued function for some values of x and then plot the real and imaginary components on the x- and y-axes, respectively. Make sure not to mix up the variable you're naming x and the x-axis on the plot. I'll use t to avoid that confusion.

import numpy as np
import matplotlib.pyplot as plt

# Input parameter.
n = 9
t = 2 * np.pi * np.arange(n) / n
# Complex valued result.
z = np.exp(1j * t)

fig, ax = plt.subplots()
ax.scatter(np.real(z), np.imag(z))
ax.set_aspect("equal")

Plot result:

Plotting imaginary numbers on a complex plane

1 Answers1