I am working with the R programming language.
I came across the following math puzzle recently:
- Suppose there is a pond with 100 fish
- Each day, there is a 5% chance that population of the pond increases by 5% of its current population
- A 5% chance that the population of the pond decreases by 5% of its current population a 90% chance that the population of the pond stays the same
I wrote some R code to represent the size of the pond over 1000 days:
set.seed(123)
n_days <- 1000
pond_population <- rep(0, n_days)
pond_population[1] <- 100
for (i in 2:n_days) {
prob <- runif(1)
if (prob <= 0.05) {
pond_population[i] <- pond_population[i-1] + round(pond_population[i-1] * 0.05)
} else if (prob > 0.05 && prob <= 0.10) {
pond_population[i] <- pond_population[i-1] - round(pond_population[i-1] * 0.05)
} else {
pond_population[i] <- pond_population[i-1]
}
}
plot(pond_population, type = "l", main = "Pond Population Over Time", xlab = "Day", ylab = "Population")
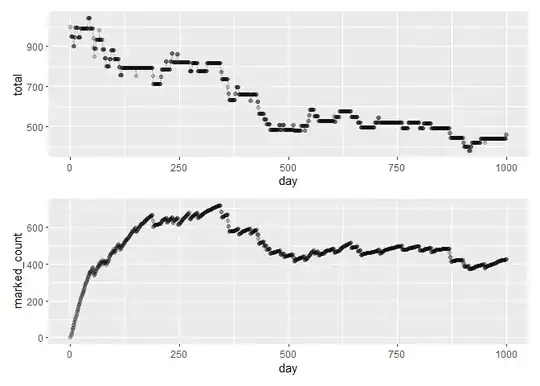
My Question: I am curious about the following modification to this problem - suppose each day you catch 10 distinct fish from this pond, tag these fish, and then put them back into the pond. Naturally, it is possible that some days you will catch fish that you previously caught in the past - and it is also possible that some of the fish you caught in the past will die. After you have finished fishing on the 1000th day - what percent of the current fish pond population will be known to you?
I am interested in learning how to write a simulation procedure to answer this question - something that can be added to code I already wrote that keeps track of the size of fish pond population each day as well as the individual fish within the pond that you have already seen (e.g. imagine if each fish is assigned a unique ID).
I am not sure how to begin this problem - I think I might have to use "stacks" or "queues" for this problem, but I am not familiar with these concepts and how they would be used here.
Can someone please show me how to do this?
Thanks!