0

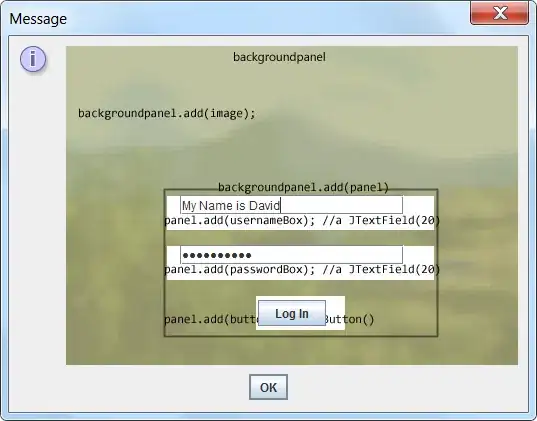
I am plotting a graph with a legend using the following command:

K = [1e3,1e4]
plt.plot(x[:len(y1)], y1, 'o', label=f'Simulation ($K_L$={K[i]:0e})')

which produces the following graph:

enter image description here

But I want the legend to be in a specific format as presented below:

KL = 103

Ro.oT
  • 623
  • 6
  • 15
KeplerNick123
  • 175
  • 6
  • You already know the base (10), so you can use `round(log10(K[i]))` to calculate the exponent, and work from there. This assumes that your numbers are all integer powers of 10, which appears to be the case. – 9769953 Jul 18 '23 at 08:03

2 Answers2

1

What about this? (insipred by this answer).

import matplotlib.pyplot as plt


def sci_notation(number: float, n_decimals: int = 2) -> str:
    sci_notation = f"{number:e}"
    decimal_part, exponent = sci_notation.split("e")
    decimal_part = float(decimal_part)
    exponent = int(exponent)

    if decimal_part == 1.0:
        return f"$10^{exponent}$"
    else:
        return f"{decimal_part:.{n_decimals}f}x$10^{exponent}$"


K = [1e3, 1.323423e4]
plt.plot([], [], "o", label=f"Simulation ($K_L$={sci_notation(K[0])})")
plt.plot([], [], "o", label=f"Simulation ($K_L$={sci_notation(K[1])})")
plt.legend()
plt.show()

enter image description here

Jordi Torrents
  • 36
  • 4
1

If your legend is hardcoded anyway, you can do this:

import numpy as np
import matplotlib.pyplot as plt

K = [1e3,1e4]  # hardcoded legend
x = np.random.rand(100)
y1 = np.random.rand(100)


plt.plot(
  x[:len(y1)],
  y1,
  'o',
  label=f'Simulation ($K_L$=$10^{int(np.log10(K[0]))}$)'
)
plt.legend()

Here the log10 of your K is put manually in the exponent (superscript).

Also, there is a scinot package that might help you formatting more flexible

import scinot as sn
a=1.7e-2
print(scinot.format(a))

1.7 × 10⁻²
Klops
  • 951
  • 6
  • 18