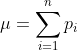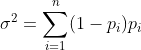The error comes from the function fitdistrplus:::checkparamlist, which is called by fitdist to ensure the names in the list passed to start match the parameter names in the function passed to distr. When you pass a vector like ppp as a parameter in start, checkparamlist renames each element of the vector by appending an integer. This means the argument names become "pp1", "pp2", "pp3" and so on up to "pp10". Since there is no argument being passed called pp, an error is thrown.
I'm not sure if there is a way to estimate vectorized parameters in fitdist due to this problem, but fortunately in this case we can easily just fit the distribution ourselves.
Since we know the mean of the distribution is
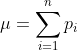
and the variance is
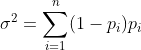
(Reference)
Then we know that if we have a sample dd, the following function will return 0 if pp fits the distribution perfectly:
objective <- function(pp) {
abs(mean(dd) - sum(pp)) + abs(sum(pp * (1 - pp)) - var(dd))
}
To demonstrate this works, let's take a much larger sample from rpoibin
set.seed(123)
dd <- poibin::rpoibin(100000, pp=seq(0.1, 0.5, length.out=10))
ppp <- runif(10)
Now we find the set of values that optimizes our objective function:
pp_opt <- optim(par = ppp, objective)$par
pp_opt
#> [1] 0.45594175 0.08754997 0.54250499 0.28056432 0.30363457 0.28354584
#> [7] 0.17861750 0.21109410 0.41562763 0.23920435
We can confirm this is a good fit by plotting a histogram and overlay the output of dpoibin with our calculated values for the pp parameter:
hist(dd, freq = FALSE, breaks = 0:11 - 0.5)
points(0:10, poibin::dpoibin(0:10, pp = pp_opt), col = "red")
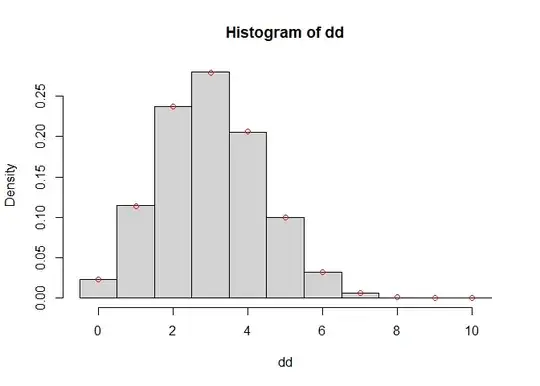
Note that there could be many solutions to the optimal value of pp, and we should not expect to get seq(0.1, 0.5, length.out = 10). For a start, order does not make a difference. We can see our pp_opt has a very similar mean and variance to seq(0.1, 0.5, length.out = 10), which is all that matters in terms of fitting the distribution
mean(seq(0.1, 0.5, length.out = 10))
#> [1] 0.3
mean(pp_opt)
#> [1] 0.2998285
sum((1 - pp_opt) * pp_opt)
#> [1] 1.930687
sum((1 - seq(0.1, 0.5, length.out = 10)) * seq(0.1, 0.5, length.out = 10))
#> [1] 1.937037
In general, it is not possible to recover pp exactly from a given sample due to the ordering and the fact that an infinite number of sets have the same distribution and calculated variance.
Created on 2023-07-18 with reprex v2.0.2