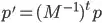17

I have a shape made out of several triangles which is positioned somewhere in world space with scale, rotate, translate. I also have a plane on which I would like to project (orthogonal) the shape.

I could multiply every vertex of every triangle in the shape with the objects transformation matrix to find out where it is located in world coordinates, and then project this point onto the plane.

But I don't need to draw the projection, and instead I would like to transform the plane with the inverse transformation matrix of the shape, and then project all the vertices onto the (inverse transformed) plane. Since it only requires me to transform the plane once and not every vertex.

My plane has a normal (xyz) and a distance (d). How do I multiply it with a 4x4 transformation matrix so that it turns out ok?

Can you create a vec4 as xyzd and multiply that? Or maybe create a vector xyz1 and then what to do with d?

Thijs Koerselman
  • 21,680
  • 22
  • 74
  • 108

3 Answers3

28

You need to convert your plane to a different representation. One where N is the normal, and O is any point on the plane. The normal you already know, it's your (xyz). A point on the plane is also easy, it's your normal N times your distance d.

Transform O by the 4x4 matrix in the normal way, this becomes your new O. You will need a Vector4 to multiply with a 4x4 matrix, set the W component to 1 (x, y, z, 1).

Also transform N by the 4x4 matrix, but set the W component to 0 (x, y, z, 0). Setting the W component to 0 means that your normals won't get translated. If your matrix is composed of more that just translating and rotating, then this step isn't so simple. Instead of multiplying by your transformation matrix, you have to multiply by the transpose of the inverse of the matrix i.e. Matrix4.Transpose(Matrix4.Invert(Transform)), there's a good explanation on why here.

You now have a new normal vector N and a new position vector O. However I suppose you want it in xyzd form again? No problem. As before, xyz is your normal N all that's left is to calculate d. d is the distance of the plane from the origin, along the normal vector. Hence, it is simply the dot product of O and N.

There you have it! If you tell me what language you're doing this in, I'd happily type it up in code as well.

EDIT, In pseudocode:

The plane is vector3 xyz and number d, the matrix is a matrix4x4 M

vector4 O = (xyz * d, 1)
vector4 N = (xyz, 0)
O = M * O
N = transpose(invert(M)) * N
xyz = N.xyz
d = dot(O.xyz, N.xyz)

xyz and d represent the new plane

Hannesh
  • 7,256
  • 7
  • 46
  • 80
  • Hi Hannesh, Thanks a lot for this clear explanation! I am doing this in Lua and C++ at the same time using differnt libraries, but the code won't be the problem. It's the concepts that I have trouble with and I think you just made it very clear. Cheers – Thijs Koerselman Oct 17 '11 at 16:34
  • Thank you, I've been struggling with this for a few evenings now. – cmannett85 Feb 20 '12 at 12:08
  • Could somebody re-write this answer in a more understandable way? Ideally with some GLM code? – Jubei Jun 20 '14 at 08:36
  • If you have scaling involved, do not forget to normalize your plane afterwards – Bluenuance Feb 06 '15 at 17:16
  • In most situations in Computer Graphics you can get away with the inverse-transpose if using column vectors or the inverse if using row vectors, but this is mathematically not correct in general (see my answer below). – Matthias Aug 07 '17 at 18:07
12

This question is a bit old but I would like to correct the accepted answer.
You do not need to convert your plane representation.

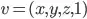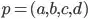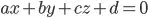
Any point v=(x,y,z,1) lies on the plane p=(a,b,c,d) if ax+by+cz+d
It can be written as dot product : pt v=0

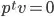
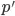You are looking for the plane p' transformed by your 4x4 matrix M.
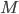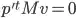
For the same reason, you must have p't Mv=0

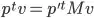So p't Mv=pt v and with some arrangements p'=M^T p

TLDR : if p=(a,b,c,d), p' = transpose(inverse(M))*p

Michael M.
  • 2,556
  • 1
  • 16
  • 26
  • Thanks, but I'm afraid I don't have the knowledge to judge your answer properly. My math skills are still rubbish and I haven't been involved in anything related since short after this question was posted. I think the only thing I can do is accept your answer and see if people will shout at me for doing so... But isn't that what Matthias was trying to explain with his answer earlier too? – Thijs Koerselman Jan 25 '18 at 16:27
  • It's probably a good idea to normalize the plane equation after doing this, especially if the matrix contains non unit basis vectors (scaling). – neeh Sep 18 '20 at 09:15
2

Notation:

  • n is a normal represented as a (1x3) row-vector
  • n' is the transformed normal of n according to transform matrix T
  • (n|d) is a plane represented as a (1x4) row-vector (with n the plane's normal and d the plane's distance to the origin)
  • (n'|d') is the transformed plane of (n|d) according to transform matrix T
  • T is a (4x4) (affine) column-major transformation matrix (i.e. transforming a column-vector t is defined as t' = T t).

Transforming a normal n:

n' = n adj(T)

Transforming a plane (n|d):

(n'|d') = (n|d) adj(T)

Here, adj is the adjugate of a matrix which is defined as follows in terms of the inverse and determinant of a matrix:

T^-1 = adj(T)/det(T)

Note:

  • The adjugate is generally not equal to the inverse of a transformation matrix T. If T includes a reflection, det(T) = -1, reversing the winding order!

  • Re-normalizing n' is mathematically not required (but maybe numerically depending on the implementation) since scaling is taken care off by the determinant. Thanks to Adrian Leonhard.

  • You can directly transform the plane without first decomposing and recomposing a plane (normal and point).
Matthias
  • 4,481
  • 12
  • 45
  • 84
  • Could you explain why using the adjugate matrix to transform a normal is correct vs the inverse transpose as derived in http://www.songho.ca/opengl/gl_normaltransform.html ? – Adrian Leonhard May 15 '18 at 18:54
  • 1
    @Leonhard I represent normals and planes as row vectors, whereas I represent points and directions as column vectors, since I use a column-major transformation matrix (see 5th dot of "notation"). If you want to use column vectors everywhere, just take the transpose of both sides of `n' = n adj(T)`, which will result in the transpose of the adjoint or alternatively the adjoint of the transpose. If you use the inverse instead of the adjoint, you will need to renormalize afterwards in case of a scaling component. Or you can divide by the determinant which is a measure of the size change. – Matthias May 16 '18 at 07:16
  • 1
    @AdrianLeonhard For a more detailed explanation/derivation see [Foundations of Game Engine Development: Volume 1: Mathematics](http://foundationsofgameenginedev.com/). Note, however, that the adjoint is some mathematical sugar in this context to obtain precise and general single-line expressions. In practice (game/rendering engine), one will multiply by the inverse transpose (or even eliminate non-uniform scaling, to multiply by the transpose transpose which is just the transformation matrix itself + renormalization due to uniform scaling). – Matthias May 16 '18 at 07:26
  • 1
    @AdrianLeonhard Furthermore, one will neither calculate the determinant nor the inverse when using a transformation/scene graph. – Matthias May 16 '18 at 07:30
  • 1
    Thanks for the clarification, but given a 2* scale transformation T = [2 0 0 0 | 0 2 0 0 | 0 0 2 0 | 0 0 0 1], adj(T) = T^-1 * det(T) = [4 0 0 0 | 0 4 0 0 | 0 0 4 0 | 0 0 0 8]. For the X = 0 plane: (1 0 0 0) * adj(T) = (4 0 0 0), which would still need to be normalized? – Adrian Leonhard May 16 '18 at 09:23
  • 1
    @AdrianLeonhard Thanks for the example. You're right normalization isn't handled by the determinant. (In fact neither the inverse nor the adjugate can know normal vectors have an extra non-linear (sqrt) restriction.) So I reread part of [FGED 1](http://foundationsofgameenginedev.com/). There are two different derivations: 1) if your normal vector is calculated as a gradient, you end up with the inverse. Since ordinary vectors (dimensions: meter) are transformed by T from A to B, whereas normal vectors (dimensions: inverse meter) are transformed by T from B to A. – Matthias May 16 '18 at 11:04
  • 1
    2) If your normal vector is calculated a cross product, you end up with an extra factor, the determinant (or alternatively, you end up with the adjugate). In both cases, you have to renormalize, making the scalar determinant obsolete if > 0. If the determinant is negative (reflection), the normal should have its direction reversed. As a general rule of thumb, everything that originates from a cross product (plane, normal, etc.) require an adjugate for transformation. – Matthias May 16 '18 at 11:08