Find the x that gives a specific value of a function

Question

I have this function:

a <- 1
b <- 2 
get_y <- function (x,a,b) {
   a * b * x
}

And I want to create a function that takes in get_y and returns the x that makes y = 4 for example. How would I do that?

So you want to solve this specific function or a more general form? If so, *how* general does it need to be? In particular, is `solve()` sufficient for your needs or do you have more complex functions? — Konrad Rudolph, Aug 15 '23 at 11:37
for the simple case, you can use `get_x <- function(y, a, b) {y / (a * b)}; get_x(4, a, b) # 2` — Mark, Aug 15 '23 at 11:38

Rui Barradas · Accepted Answer · 2023-08-15T16:24:49.737

3

You can solve

get_y(x,a,b) - 4 == 0

with uniroot. You don't have to create a new function, an anonymous one will do it.

a <- 1
b <- 2 
get_y <- function (x,a,b) {
  a * b * x
}

uniroot(\(x) get_y(x,a,b) - 4, c(0, 10))
#> $root
#> [1] 2
#> 
#> $f.root
#> [1] 0
#> 
#> $iter
#> [1] 1
#> 
#> $init.it
#> [1] NA
#> 
#> $estim.prec
#> [1] 8

^{Created on 2023-08-15 with reprex v2.0.2}

Edit

Following ThomasIsCoding's comment, here is a heuristic I many times use to find the search limits.

When the functions are (relatively) simple, use curve to plot the function. If I get it wrong at the first try, expand the limits until I no longer do. In this case, it was at the 2nd try.

# doesn't display the horizontal line,
# the intersection between the function and the line y = 4
# must be outside the plot's y axis range
# curve(get_y(x, a = a, b = b), from = 0, to = 1)

# now yes, there's an intersection, the uniroot 
# search limits can be set to the interval [0, 10]
curve(get_y(x, a = a, b = b), from = 0, to = 10)
abline(h = 4)

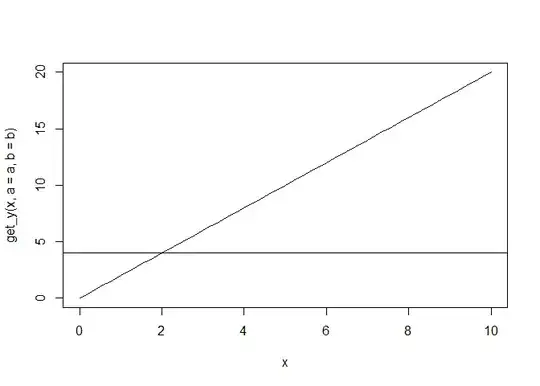
^{Created on 2023-08-15 with reprex v2.0.2}

edited Aug 15 '23 at 16:24

answered Aug 15 '23 at 11:39

Rui Barradas

70,273
8
34
66

`uniroot` or `optimize` are powerful tools, +1! The only concern for those numeric methods is that we may have no idea about what is the feasible range for `x` to search the root. For example, here you assumed `c(-10, 10)` and the code works, but sometimes you may have no idea about what is the domain of `get_x` if there are some constraints. – ThomasIsCoding Aug 15 '23 at 12:24
I actually get an error: Error: unexpected symbol in "uniroot((x) get_y" – Victor Nielsen Aug 15 '23 at 12:37
@VictorNielsen What version of R are you using? That error many times comes from the new lambdas introduced in R 4.1 (2021-05-18). Try `function(x)` instead of ```\(x)```. – Rui Barradas Aug 15 '23 at 13:10
That solved it! – Victor Nielsen Aug 15 '23 at 14:42
@VictorNielsen Time to update R? – Rui Barradas Aug 15 '23 at 16:15
@ThomasIsCoding You are right. I have edited the answer with a (very) crude way of finding the limits, which are different from the original answer's, btw. – Rui Barradas Aug 15 '23 at 16:27
1

Good reminder to do it. Thought my version was more recent, but you are right, it's from 2020. – Victor Nielsen Aug 15 '23 at 16:27

ThomasIsCoding · Answer 2 · 2023-08-15T12:20:47.110

You can try Ryacas like below

library(Ryacas)
y <- 4
f <- sprintf("%s-%s", gsub("\\{|\\}", "", deparse1(body(get_y))), y)
x <- solve(ysym(f), "x")

and you will obtain

> x
{x==4/(a*b)}

If you want numeric solution of x, you can try the code below with a few more lines

get_x <- function(get_y, y, a, b) {
    f <- sprintf("%s-%s", gsub("\\{|\\}", "", deparse1(body(get_y))), y)
    s <- gsub("x==", "", solve(ysym(f), "x"))
    y_eval(yac_expr(s), a = a, b = b, as.r = TRUE)
}

such that

> get_x(get_y, 4, a, b)
[1] 2

> get_x(get_y, 4, a, 5)
[1] 0.8

Find the x that gives a specific value of a function

2 Answers2

Edit