Largest rectangular sub matrix with the same number

Question

I am trying to come up with a dynamic programming algorithm that finds the largest sub matrix within a matrix that consists of the same number:

example:

{5 5 8}
{5 5 7}
{3 4 1}

Answer : 4 elements due to the matrix

   5 5 
   5 5   

Answer 1

This is a question I already answered here (and here, modified version). In both cases the algorithm was applied to binary case (zeros and ones), but the modification for arbitrary numbers is quite easy (but sorry, I keep the images for the binary version of the problem). You can do this very efficiently by two pass linear O(n) time algorithm - n being number of elements. However, this is not a dynamic programming - I think using dynamic programming here would be clumsy and inefficient in the end, because of the difficulties with problem decomposition, as the OP mentioned - unless its a homework - but in that case you can try to impress by this algorithm :-) as there's obviously no faster solution than O(n).

Algorithm (pictures depict binary case):

Say you want to find largest rectangle of free (white) elements.

Here follows the two pass linear O(n) time algorithm (n being number of elemets):

1) in a first pass, go by columns, from bottom to top, and for each element, denote the number of consecutive elements available up to this one:

repeat, until:

Pictures depict the binary case. In case of arbitrary numbers you hold 2 matrices - first with the original numbers and second with the auxiliary numbers that are filled in the image above. You have to check the original matrix and if you find a number different from the previous one, you just start the numbering (in the auxiliary matrix) again from 1.

2) in a second pass you go by rows, holding data structure of potential rectangles, i.e. the rectangles containing current position somewhere at the top edge. See the following picture (current position is red, 3 potential rectangles - purple - height 1, green - height 2 and yellow - height 3):

For each rectangle we keep its height k and its left edge. In other words we keep track of the sums of consecutive numbers that were >= k (i.e. potential rectangles of height k). This data structure can be represented by an array with double linked list linking occupied items, and the array size would be limited by the matrix height.

Pseudocode of 2nd pass (non-binary version with arbitrary numbers):

var m[] // original matrix
var aux[] // auxiliary matrix filled in the 1st pass
var rect[] // array of potential rectangles, indexed by their height
           // the occupied items are also linked in double linked list, 
           // ordered by height

foreach row = 1..N // go by rows
    foreach col = 1..M
        if (col > 1 AND m[row, col] != m[row, col - 1]) // new number
            close_potential_rectangles_higher_than(0);  // close all rectangles

        height = aux[row, col] // maximal height possible at current position

        if (!rect[height]) { // rectangle with height does not exist
            create rect[height]    // open new rectangle
            if (rect[height].next) // rectangle with nearest higher height
                                   // if it exists, start from its left edge
                rect[height].left_col = rect[height].next.left_col
            else
                rect[height].left_col = col; 
        }

        close_potential_rectangles_higher_than(height)
    end for // end row
    close_potential_rectangles_higher_than(0);
        // end of row -> close all rect., supposing col is M+1 now!

end for // end matrix

The function for closing rectangles:

function close_potential_rectangles_higher_than(height)
    close_r = rectangle with highest height (last item in dll)
    while (close_r.height > height) { // higher? close it
        area = close_r.height * (col - close_r.left_col)
        if (area > max_area) { // we have maximal rectangle!
            max_area = area
            max_topleft = [row, close_r.left_col]
            max_bottomright = [row + height - 1, col - 1]
        }
        close_r = close_r.prev
        // remove the rectangle close_r from the double linked list
    }
end function

This way you can also get all maximum rectangles. So in the end you get:

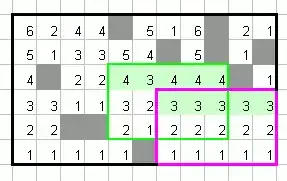
And what the complexity will be? You see that the function close_potential_rectangles_higher_than is O(1) per closed rectangle. Because for each field we create 1 potential rectangle at the maximum, the total number of potential rectangles ever present in particular row is never higher than the length of the row. Therefore, complexity of this function is O(1) amortized!

So the whole complexity is O(n) where n is number of matrix elements.

Answer 2

A dynamic solution:

Define a new matrix A wich will store in A[i,j] two values: the width and the height of the largest submatrix with the left upper corner at i,j, fill this matrix starting from the bottom right corner, by rows bottom to top. You'll find four cases:

case 1: none of the right or bottom neighbour elements in the original matrix are equal to the current one, i.e: M[i,j] != M[i+1,j] and M[i,j] != M[i,j+1] being M the original matrix, in this case, the value of A[i,j] is 1x1

case 2: the neighbour element to the right is equal to the current one but the bottom one is different, the value of A[i,j].width is A[i+1,j].width+1 and A[i,j].height=1

case 3: the neighbour element to the bottom is equal but the right one is different, A[i,j].width=1, A[i,j].height=A[i,j+1].height+1

case 4: both neighbours are equal: A[i,j].width = min(A[i+1,j].width+1,A[i,j+1].width) and A[i,j].height = min(A[i,j+1]+1,A[i+1,j])

the size of the largest matrix that has the upper left corner at i,j is A[i,j].width*A[i,j].height so you can update the max value found while calculating the A[i,j]

the bottom row and the rightmost column elements are treated as if their neighbours to the bottom and to the right respectively are different

in your example, the resulting matrix A would be:

{2:2 1:2 1:1}
{2:1 1:1 1:1}
{1:1 1:1 1:1}

being w:h width:height

Answer 3

Modification to the above answer:

Define a new matrix A wich will store in A[i,j] two values: the width and the height of the largest submatrix with the left upper corner at i,j, fill this matrix starting from the bottom right corner, by rows bottom to top. You'll find four cases:

case 1: none of the right or bottom neighbour elements in the original matrix are equal to the current one, i.e: M[i,j] != M[i+1,j] and M[i,j] != M[i,j+1] being M the original matrix, in this case, the value of A[i,j] is 1x1

case 2: the neighbour element to the right is equal to the current one but the bottom one is different, the value of A[i,j].width is A[i+1,j].width+1 and A[i,j].height=1

case 3: the neighbour element to the bottom is equal but the right one is different, A[i,j].width=1, A[i,j].height=A[i,j+1].height+1

case 4: both neighbours are equal: Three rectangles are considered: 1. A[i,j].width=A[i,j+1].width+1; A[i,j].height=1;

1. A[i,j].height=A[i+1,j].height+1; a[i,j].width=1;

2. A[i,j].width = min(A[i+1,j].width+1,A[i,j+1].width) and A[i,j].height = min(A[i,j+1]+1,A[i+1,j])

The one with the max area in the above three cases will be considered to represent the rectangle at this position.

The size of the largest matrix that has the upper left corner at i,j is A[i,j].width*A[i,j].height so you can update the max value found while calculating the A[i,j]

the bottom row and the rightmost column elements are treated as if their neighbours to the bottom and to the right respectively are different.

Answer 4

This question is a duplicate. I have tried to flag it as a duplicate. Here is a Python solution, which also returns the position and shape of the largest rectangular submatrix:

#!/usr/bin/env python3

import numpy

s = '''5 5 8
5 5 7
3 4 1'''

nrows = 3
ncols = 3
skip_not = 5
area_max = (0, [])

a = numpy.fromstring(s, dtype=int, sep=' ').reshape(nrows, ncols)
w = numpy.zeros(dtype=int, shape=a.shape)
h = numpy.zeros(dtype=int, shape=a.shape)
for r in range(nrows):
    for c in range(ncols):
        if not a[r][c] == skip_not:
            continue
        if r == 0:
            h[r][c] = 1
        else:
            h[r][c] = h[r-1][c]+1
        if c == 0:
            w[r][c] = 1
        else:
            w[r][c] = w[r][c-1]+1
        minw = w[r][c]
        for dh in range(h[r][c]):
            minw = min(minw, w[r-dh][c])
            area = (dh+1)*minw
            if area > area_max[0]:
                area_max = (area, [(r, c, dh+1, minw)])

print('area', area_max[0])
for t in area_max[1]:
    print('coord and shape', t)

Output:

area 4
coord and shape (1, 1, 2, 2)