clustering data outputs irregular plot graph

Question

Ok I will run down what im trying to achieve and how I tryed to achieve it then I will explain why I tryed this method.

I have data from the KDD cup 1999 in its original format the data has 494k of rows with 42 columns.

My goal is trying to cluster this data unsupervised. From a previous question here:

clustering and matlab

I recieved this feedback:

For starters, you need to normalize the attributes to be of the same scale: when computing the euclidean distance as part of step 3 in your method, the features with values such as 239 and 486 will dominate over the other features with small values as 0.05, thus disrupting the result.

Another point to remember is that too many attributes can be a bad thing (curse of dimensionality). Thus you should look into feature selection or dimensionality reduction techniques.

So the first thing I went about doing was addressing the feature selection which is related to this article: http://narensportal.com/papers/datamining-classification-algorithm.aspx#_sec-2-1

and looks like this after selecting the necessary features:

So for the clustering I removed the discrete values which left me with 3 columns with numeric data, I then went about removing the duplicate rows see: junk, index and unique on a matrix (how to keep matrix format) in the file which reduced the 3 columns from 494k to 67k which was done like so:

[M,ind] = unique(data, 'rows', 'first');
[~,ind] = sort(ind);
M = M(ind,:);

I then used the random permutation to reduce the file size from 67k to 1000 like so:

m = 1000;
n = 3;

%# pick random rows
indX = randperm( size(M,1) );
indX = indX(1:m);

%# pick random columns
indY = randperm( size(M,2) );
indY = indY(1:n);

%# filter data
data = M(indX,indY)

So now I have a file with 3 of my features which I selected I have removed duplicate records and used the random permutation to further reduce the dataset my last goal was to normalize this data and I did this with:

normalized_data = data/norm(data);

I then used the following K-means script:

%% generate clusters
K = 4;

%% cluster
opts = statset('MaxIter', 500, 'Display', 'iter');
[clustIDX, clusters, interClustSum, Dist] = kmeans(data, K, 'options',opts, ...
'distance','sqEuclidean', 'EmptyAction','singleton', 'replicates',3);

%% plot data+clusters
figure, hold on
scatter3(data(:,1),data(:,2),data(:,3), 50, clustIDX, 'filled')
scatter3(clusters(:,1),clusters(:,2),clusters(:,3), 200, (1:K)', 'filled')
hold off, xlabel('x'), ylabel('y'), zlabel('z')
%% plot clusters quality
figure
[silh,h] = silhouette(data, clustIDX);
avrgScore = mean(silh);

%% Assign data to clusters
% calculate distance (squared) of all instances to each cluster centroid
D = zeros(numObservarations, K);     % init distances
for k=1:K
%d = sum((x-y).^2).^0.5
D(:,k) = sum( ((data - repmat(clusters(k,:),numObservarations,1)).^2), 2);
end

% find  for all instances the cluster closet to it
[minDists, clusterIndices] = min(D, [], 2);
% compare it with what you expect it to be
sum(clusterIndices == clustIDX)

But my results are still coming out like my original question I asked here: clustering and matlab

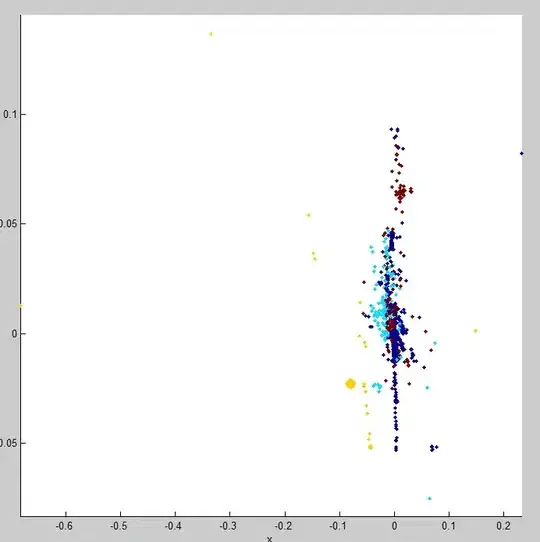
Here is what the data looks like when plotted:

and:

Can anyone help solve this problem, are the methods im using not the correct methods or is there something im missing?

Answer 1

Just like to say thanks to cyborg and Amro for helping, I realized that rather than create my own pre-processing I kept the dimensions as such and I finally managed to get some clustered data!

Out put!

Ofcourse I still have some outliers but if I could get rid of them and plot the graph from -0.2 - 0.2 im sure it would look alot better. But if you look at the original attempt I seem to be getting there!

  %% load data
    %# read the list of features
    fid = fopen('kddcup.names','rt');
    C = textscan(fid, '%s %s', 'Delimiter',':', 'HeaderLines',1);
    fclose(fid);

    %# determine type of features
    C{2} = regexprep(C{2}, '.$','');              %# remove "." at the end
    attribNom = [ismember(C{2},'symbolic');true]; %# nominal features

    %# build format string used to read/parse the actual data
    frmt = cell(1,numel(C{1}));
    frmt( ismember(C{2},'continuous') ) = {'%f'}; %# numeric features: read as number
    frmt( ismember(C{2},'symbolic') ) = {'%s'};   %# nominal features: read as string
    frmt = [frmt{:}];
    frmt = [frmt '%s'];                           %# add the class attribute

    %# read dataset
    fid = fopen('kddcup.data_10_percent_corrected','rt');
    C = textscan(fid, frmt, 'Delimiter',',');
    fclose(fid);

    %# convert nominal attributes to numeric
    ind = find(attribNom);
    G = cell(numel(ind),1);
    for i=1:numel(ind)
        [C{ind(i)},G{i}] = grp2idx( C{ind(i)} );
    end

    %# all numeric dataset
    fulldata = cell2mat(C);
    %% dimensionality reduction 
    columns = 42
    [U,S,V]=svds(fulldata,columns)
    %% randomly select dataset
    rows = 5000;
    %# pick random rows
    indX = randperm( size(fulldata,1) );
    indX = indX(1:rows);
    %# pick random columns
    indY = randperm( size(fulldata,2) );
    indY = indY(1:columns);
    %# filter data
    data = U(indX,indY)
    %% apply normalization method to every cell
    data = data./repmat(sqrt(sum(data.^2)),size(data,1),1)
    %% generate sample data
    K = 4;
    numObservarations = 5000;
    dimensions = 42;
    %% cluster
    opts = statset('MaxIter', 500, 'Display', 'iter');
    [clustIDX, clusters, interClustSum, Dist] = kmeans(data, K, 'options',opts, ...
    'distance','sqEuclidean', 'EmptyAction','singleton', 'replicates',3);
    %% plot data+clusters
    figure, hold on
    scatter3(data(:,1),data(:,2),data(:,3), 5, clustIDX, 'filled')
    scatter3(clusters(:,1),clusters(:,2),clusters(:,3), 100, (1:K)', 'filled')
    hold off, xlabel('x'), ylabel('y'), zlabel('z')
    %% plot clusters quality
    figure
    [silh,h] = silhouette(data, clustIDX);
    avrgScore = mean(silh);
    %% Assign data to clusters
    % calculate distance (squared) of all instances to each cluster centroid
    D = zeros(numObservarations, K);     % init distances
    for k=1:K
    %d = sum((x-y).^2).^0.5
    D(:,k) = sum( ((data - repmat(clusters(k,:),numObservarations,1)).^2), 2);
    end
    % find  for all instances the cluster closet to it
    [minDists, clusterIndices] = min(D, [], 2);
    % compare it with what you expect it to be
    sum(clusterIndices == clustIDX)

Answer 2

You have a problem in the normalization: data/norm(data);. What you probably need to do is to use: data_normed = data./repmat(sqrt(sum(data.^2)),size(data,1),1). This computes the norm of every column of data, then it duplicates the answer to the original size of data, then it divides data by the norms of the columns.

Comment:

A better way to reduce the dimensionality of the number of features is [U,S,V]=svd(data); U=U(:,1:m) or for sparse data [U,S,V]=svds(data,m). It might loose some information in the way, but it's much better than random picking.