20

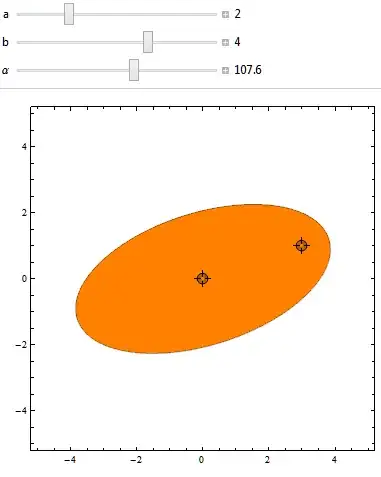
How to test if a point P = [xp,yp] is inside/outside some rotated ellipse given by the centre C=[x,y], a, b, and phi ( angle of rotation)?

At this moment I am using the following solution: rotate ellipse and point by the angle -phi and then the common test for a position of the point and "non rotated" ellipse.

But there are a lot of tested points (thousands) and I find this solution as slow. Is there any direct and more efficient way to get a position of the rotated ellipse and point?

I do not need a code but the algorithm. Thanks for your help.

justik
  • 4,145
  • 6
  • 32
  • 53

5 Answers5

47

Another option is just to throw everything into the equation for a 2D rotated ellipse and see if the result is less than one.

So a point is inside the ellipse if the following inequality is true

ellipse equation

Where (xp,yp) are the point coordinates and (x0, y0) is the center of the ellipse.

I implemented a small Mathematica program demonstrating that this indeed works: Manipulate screen shot

Here it is in action:

Animation

And here is the code:

ellipse[x_, y_, a_, b_, \[Alpha]_, x0_: 0, y0_: 0] := 
     (((x - x0)*Cos[\[Alpha]] + (y - y0)*Sin[\[Alpha]])/a)^2
   + (((x - x0)*Sin[\[Alpha]] - (y - y0)*Cos[\[Alpha]])/b)^2;

Manipulate[
 RegionPlot[
  ellipse[x, y, a, b, \[Alpha] \[Degree], Sequence @@ pos] < 1, {x, -5, 5}, {y, -5, 5}, 
  PlotStyle -> If[ellipse[Sequence @@ p, a, b, \[Alpha] \[Degree], Sequence @@ pos] <= 1, Orange, LightBlue], 
  PlotPoints -> 25]
, {{a, 2}, 1, 5, Appearance -> "Labeled"}
, {{b, 4}, 2, 5, Appearance -> "Labeled"}
, {\[Alpha], 0, 180,  Appearance -> "Labeled"}
, {{p, {3, 1}}, Automatic, ControlType -> Locator}
, {{pos, {0, 0}}, Automatic, ControlType -> Locator}]
Ajasja
  • 809
  • 1
  • 16
  • 21
14

You can simply feed your data into the formula stated above. Here is a python implementation I made on Ajasja's recommendations:

def pointInEllipse(x,y,xp,yp,d,D,angle):
    #tests if a point[xp,yp] is within
    #boundaries defined by the ellipse
    #of center[x,y], diameter d D, and tilted at angle

    cosa=math.cos(angle)
    sina=math.sin(angle)
    dd=d/2*d/2
    DD=D/2*D/2

    a =math.pow(cosa*(xp-x)+sina*(yp-y),2)
    b =math.pow(sina*(xp-x)-cosa*(yp-y),2)
    ellipse=(a/dd)+(b/DD)

    if ellipse <= 1:
        return True
    else:
        return False
msc
  • 3,780
  • 1
  • 22
  • 27
Raoul
  • 1,872
  • 3
  • 26
  • 48
  • 1
    Don't use `math.pow(val, 2)` to square something. That's really slow. (Assign it to a variable and multiply that by itself). – Peter Cordes Mar 15 '17 at 10:27
  • 2
    `math.sin` and `math.cos` expect their arguments in radians so make sure you are passing the angle in radians. You can use `math.radians` function to convert from degrees to radians. – Q2Learn Feb 15 '21 at 14:41
9

To deal with ellipses I prefer to transform them to another coordinate system where the ellipse is a unit circle centered at the origin.

If you see the ellipse as a unit circle (radius 1), scaled by (a,b), rotated by phi and transformed by (x,y), then life becomes a lot easier. If you have that transform matrix you can use it to do an easier containment query. If you transform the point to be in the coordinate system where the ellipse is a unit circle, all you have to do is a point-in-unit circle test which is trivial. If "transform" is a matrix that transforms a unit circle into your ellipse as described, then

transformedPoint = transform.Invert().Transform(point);
pointInEllipse = transformedPoint.DistanceTo(0,0) < 1.0;
Anders Forsgren
  • 10,827
  • 4
  • 40
  • 77
1

Here is the algorithm, I let you develop the code:

  1. Determine the vector v1 between the center of ellipse and your point
  2. Determine angle a1 between vector v1 and x axis in world coordinates
  3. Substract phi from a1 to get a2, our vector angle in local coordinates
  4. Determine point P2 on ellipse at angle a2 in local coordinates, not offset by (x, y)
  5. Compute L1 and L2, the vector length of a1 and a2

Evaluation:

  1. If L1 < L2 the point is inside
  2. If L1 = L2 (plus/minus a small tolerance) the point is on the ellipse
  3. If L2 > L2 the point is outside

Ellipse parametric formula:

x = a*cos(u)
y = b*sin(u)

valid for u between -pi and +pi. Add phi to u to rotate your ellipse.

The algorithm above can be simplified and optimized from ellipse equations.

Good luck!

rjobidon
  • 3,055
  • 3
  • 30
  • 36
0

Matplotlib has an Ellipse method within the patches class, that allows you to ask the question if a point is inside or out of the patch. Check here and look for the method contains_point(). You will need to create the ellipse with the Ellipse class, and then as if there is a point inside. BTW, matplotlib is a package for python.

Jose Sergio Hleap
  • 1
  • 1