Profiling Mathematica Code

Question

Is there a good way to profile code in Mathematica? I would like to be able to recurse (i.e., if I say f[a_] := b[a], then Profile[f[1]] should give almost the same output as Profile[b[1]]), but I'll settle for being able to do something like applying Timing to every relevant subexpression. It would be nice if I didn't have to special-case things like Module, but I'd like, e.g., Profile[Module[{x=1+2},x!]] to give me an output like

Time    Expression         Result
0       1                  1
0       2                  2
0       1 + 2              3
0       x$1234             3   
0       x$1234 !           6
0       Module[{x=1+2},x!] 6

6

Related: http://stackoverflow.com/questions/3418892/profiling-memory-usage-in-mathematica — abcd, Nov 11 '11 at 01:53
Also see: http://stackoverflow.com/questions/4721171/performance-tuning-in-mathematica — Mr.Wizard, Nov 11 '11 at 05:23
All: I am trying to do this with `TraceScan` but I am running into the problem that Mathematica caches results, therefore sequential calls to `Prime[13!]` for example take greatly different times to evaluate. — Mr.Wizard, Nov 11 '11 at 05:42

score 5 · Answer 1 · edited Nov 16 '11 at 10:15

Yes, Wolfram Workbench does have a profiler, although according to the documentation the output isn't quite in the form you want.

I should note that the issue raised by Mr.Wizard in comments - that cached results will lead to different timing results - can also apply in profile.

If you wanted to do something exclusively in Mathematica, you could try something like:

myProfile[fun_Symbol,inputs_List]:=  
    TableForm[#[[{1,3,2}]]&/@ (Join @@@ ({Timing[f[#]],#} & /@ inputs))]

If you were happy enough to have the output as {timing,output, input}, rather than {timing, input, output} as specified in your question, you could get rid of the #[[{1,3,2}]] bit.

EDIT

Since I have Workbench, here is an example. I have a package AdvancedPlots which includes a function CobwebPlot (and yes, the function itself could improved).

CobwebPlot[x_?MatrixQ, opts___Rule] /; 
  And @@ (NumericQ /@ Flatten[x]) :=   
 Module[{n, \[Theta]s, numgrids, grids, struts, gridstyle, min, max, 
   data, labels, epilabels, pad},
  n = Length[First[x]];
  \[Theta]s = (2 \[Pi])/n Range[0, n] + If[OddQ[n], \[Pi]/2, 0];
  numgrids = 
   If[IntegerQ[#] && Positive[#], #, 
      NumberofGrids /. 
       Options[CobwebPlot] ] & @ (NumberofGrids /. {opts});
  {min, max} = {Min[#], Max[#]} &@ Flatten[x];
  gridstyle = GridStyle /. {opts} /. Options[CobwebPlot];
  pad = CobwebPadding /. {opts} /. Options[CobwebPlot];
  grids = 
   Outer[List, \[Theta]s, FindDivisions[{0, max + 1}, numgrids]];
  struts = Transpose[grids];
  labels = CobwebLabels /. {opts} /. Options[CobwebPlot];
  epilabels = 
   If[Length[labels] == n, 
    Thread[Text[
      labels, (1.2 max) Transpose[{Cos[Most[\[Theta]s]], 
         Sin[Most[\[Theta]s]]}]]], None];
  data = Map[Reverse, 
    Inner[List, Join[#, {First[#]}] & /@ x, \[Theta]s, List], {2}];
  Show[ListPolarPlot[grids, gridstyle, Joined -> True, Axes -> False, 
    PlotRangePadding -> pad], 
   ListPolarPlot[struts, gridstyle, Joined -> True, Axes -> False], 
   ListPolarPlot[data, 
    Sequence @@ FilterRules[{opts}, Options[ListPolarPlot]], 
    Sequence @@ 
     FilterRules[Options[CobwebPlot], Options[ListPolarPlot]], 
    Joined -> True, Axes -> None] , 
   If[Length[labels] == n, Graphics /@ epilabels, 
    Sequence @@ FilterRules[{opts}, Options[Graphics]] ]]
  ]

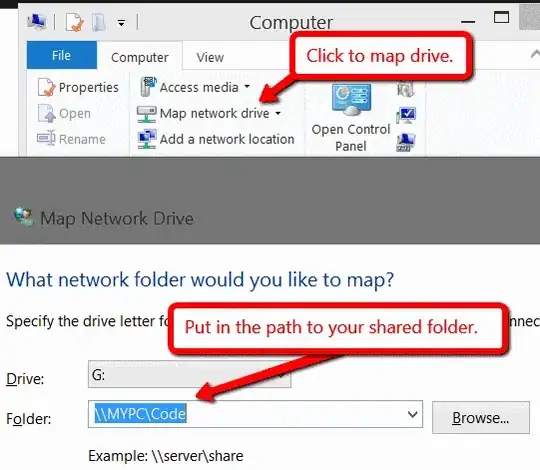
Running the package in Debug mode

And then running this notebook

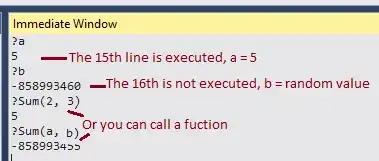
enter image description here

Gives the following output.

If you feel that this function can be improved, why not post it on Code Review? — Mr.Wizard, Nov 13 '11 at 16:35
This is almost what I'm looking for, but Profile seems to miss most of my code. The code I'm trying to profile right now takes 63 seconds to execute (according to Timing), but the biggest contributions to the profile are 90 calls to MakeBoxes[Peak:PeakObject[_List],FormatType_] with time 0.718 (each? total?) and 723344 calls to 7 with with 0.655 (each? total?). Also, something like Profile[Do[100000!, {100}]] doesn't give any entries in the profile at all. — Jason Gross, Nov 26 '11 at 18:43

score 4 · Answer 2 · answered Nov 11 '11 at 16:55

This is an attempt to use TraceScan to time individual steps of evaluation. It uses raw AbsoluteTime[] deltas which could be good or bad depending on what you actually expect to time.

Make sure to run this example on a fresh kernel, or Prime will cache its results and all timings will be ~= 0.

t = AbsoluteTime[]; step = "start";

TraceScan[
  (Print[AbsoluteTime[] - t, " for ", step]; t = AbsoluteTime[]; step = #) &,
  Module[{x = 7 + 7}, Sqrt@Prime[x!]]
]

0.0010001 for start

0.*10^-8 for Module[{x=7+7},Sqrt[Prime[x!]]]

0.*10^-8 for Module

0.*10^-8 for 7+7

0.*10^-8 for Plus

0.*10^-8 for 7

0.*10^-8 for 7

0.*10^-8 for 14

0.*10^-8 for x$149=Unevaluated[14]

0.*10^-8 for Set

0.*10^-8 for x$149=14

0.*10^-8 for 14

0.*10^-8 for Sqrt[Prime[x$149!]]

0.*10^-8 for Sqrt

0.*10^-8 for Prime[x$149!]

0.*10^-8 for Prime

0.*10^-8 for x$149!

0.*10^-8 for Factorial

0.*10^-8 for x$149

0.*10^-8 for 14

0.*10^-8 for 14!

0.*10^-8 for 87178291200

2.6691526 for Prime[87178291200]

0.*10^-8 for 2394322471421

0.*10^-8 for Sqrt[2394322471421]

0.*10^-8 for Sqrt[2394322471421]

0.*10^-8 for Power

0.*10^-8 for 2394322471421

0.*10^-8 for 1/2

score 1 · Answer 3 · answered Nov 11 '11 at 05:26

1

As belisarius showed in answer to the question I linked above, it appears that Wolfram Workbench includes a profiler. I do not use Workbench however, so I cannot detail its use.

answered Nov 11 '11 at 05:26

Mr.Wizard

24,179
5
44
125

Profiling Mathematica Code

3 Answers3