I have a CLLocationCoordinate2D (c1) and a CLLocation (l1), so I have lat/long values for each point and I can calculate the distance in meters between them using:
[c1 distanceFromLocation:l1]
How can I find the coordinates of a point (c2) 100 meters closer to l1 than c1 (along the same bearing)?
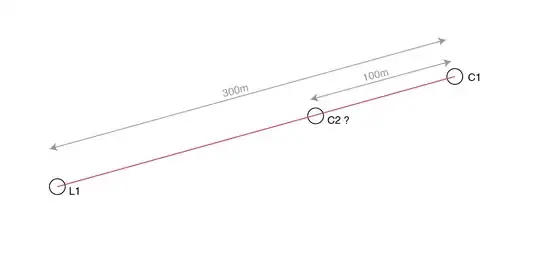
I have calculated it using basic trig using the following:
- used the difference in latitude and longitude to calculate the hypotenuse and angle
- used the ratio between the distance to cl and the distance to c2 to get the hypotenuse of a triangle ending at c2
- used cos and sin to calculate the longitude and latitude of c2
But this seems like a hacky way of doing it as it doesn't take into account of curvature and seems to be using latitude and longitude in a way they are not supposed to be used. It does seem to work over short distances though.