pseudo-random pattern with fixed density and exclusion zone

Question

I wish to create a 2D set of N points (typically 1e2 - 1e4) in a square with the following constraints:

there should be a minimal distance between all points (hard core exclusion zone)
the number of points filling the square is given in advance (or a close estimate), as I want to obtain a fixed density (I can adjust a little the size of the square afterwards if necessary).
the pattern should be reasonably "random"
a fast solution is preferred

I used rStrauss in the package spatstat before, but i could never figure out how to reliably obtain a given number of points, and quite often the function would stall my machine for 10 minutes, presumably because the task was too hard. I'm guessing there may be a more suitable function for this.

## regular grid of 1e2 points in [-10, 10]^2
xy = expand.grid(x=seq(-10, 10, length=10), y=seq(-10, 10, length=10))
N = NROW(xy)

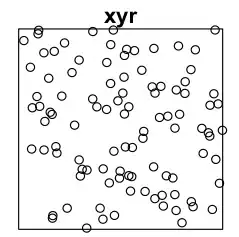
EDIT: as suggested in the answer

xyr = rSSI(r=0.1, N, win = owin(c(-10,10),c(-10,10)), N)
plot(xyr)

score 3 · Accepted Answer · answered Nov 19 '11 at 22:35

rSSI, also in the spatstat package, takes care of your issues, except possibly the speed, depending on your standards. It has a hardcore inhibition distance, and will hit a target number of points (or give up trying--you can set the threshold for giving up), and the placements are random. I don't think it's particularly fast, but I was able to create 1e6 points in the unit square with an inhibition distance of 1e-4 in about 30 seconds. The speed and success rate will depend heavily on your inhibition distance relative to the number of points.

Interesting problem. I'd be curious about what is the most efficient algorithm, in general. Thanks for the links! — John Colby, Nov 19 '11 at 22:40

John Colby · Answer 2 · 2011-11-21T16:22:42.027

Mostly as an excuse to learn some more about Rcpp, here is my attempt at a little function to do this:

require(inline)
require(Rcpp)

randPoints = cxxfunction(signature(r_n='int', r_mindist='float', r_maxiter='int'), body = 
' 
  using namespace std;

  int n = as<int> (r_n);
  float mindist = as<float> (r_mindist);
  int maxiter = as<int> (r_maxiter);

  RNGScope scope;
  bool tooclose;
  int iter;
  NumericVector rands (2);
  NumericMatrix points (n, 2);
  NumericVector dist (2);

  for (int i=0; i < n; i++) {
    iter = 0;
    do {
      iter++;
      tooclose = false;
      rands = runif(2, 0, 1);
      for (int idist=0; idist < i; idist++) {
        dist = rands - points(idist, _);
        dist = dist * dist;
        if (sqrt(accumulate(dist.begin(), dist.end(), 0.0)) < mindist) {
          tooclose = true;
          break;
        }
      }
    } while (tooclose & iter < maxiter);
    if (iter == maxiter) {
      Rprintf("%d iterations reached\\nOnly %d points found\\n", maxiter, i+1);
      break;
    }
    NumericMatrix::Row target(points, i);
    target = rands;
  }

  return(wrap(points));
'
, plugin='Rcpp')

Then you can use it like:

> x = randPoints(1000, 0.05, 10000)
10000 iterations reached
Only 288 points found

And here is the plot:

x = x[as.logical(rowMeans(x != 0)), ]
dev.new(width=4, height=4)
plot(x)

enter image description here

pseudo-random pattern with fixed density and exclusion zone

2 Answers2