I have been given an assignment to simulate an NFA in Java. Now the following regular expression that I have to simulate an NFA for is
ab*((b|d)|c*)
I think I have too many e-symbols. I was just wondering if the following image below is correct.
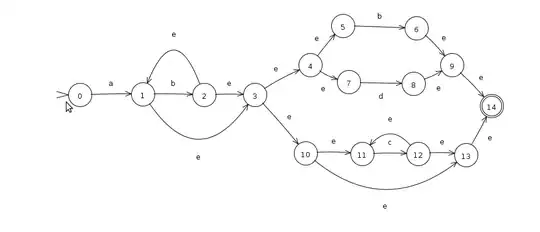
I have been given an assignment to simulate an NFA in Java. Now the following regular expression that I have to simulate an NFA for is
ab*((b|d)|c*)
I think I have too many e-symbols. I was just wondering if the following image below is correct.

Your NFA graph is correct. It will match the regex ab*((b|d)|c*) and nothing else. However, it could be much simpler, e.g. like this: