How can I speed up this call to quantile in Matlab?

Question

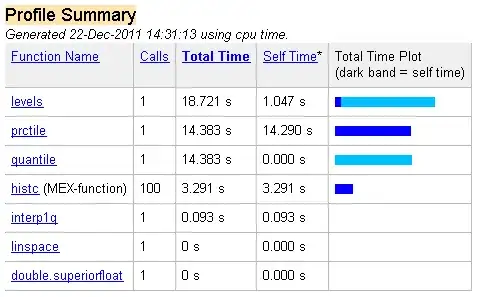
I have a MATLAB routine with one rather obvious bottleneck. I've profiled the function, with the result that 2/3 of the computing time is used in the function levels:

The function levels takes a matrix of floats and splits each column into nLevels buckets, returning a matrix of the same size as the input, with each entry replaced by the number of the bucket it falls into.

To do this I use the quantile function to get the bucket limits, and a loop to assign the entries to buckets. Here's my implementation:

function [Y q] = levels(X,nLevels)
% "Assign each of the elements of X to an integer-valued level"

p = linspace(0, 1.0, nLevels+1);

q = quantile(X,p);
if isvector(q)
    q=transpose(q);
end

Y = zeros(size(X));

for i = 1:nLevels
    % "The variables g and l indicate the entries that are respectively greater than
    % or less than the relevant bucket limits. The line Y(g & l) = i is assigning the
    % value i to any element that falls in this bucket."
    if i ~= nLevels % "The default; doesnt include upper bound"
        g = bsxfun(@ge,X,q(i,:));
        l = bsxfun(@lt,X,q(i+1,:));
    else            % "For the final level we include the upper bound"
        g = bsxfun(@ge,X,q(i,:));
        l = bsxfun(@le,X,q(i+1,:));
    end
    Y(g & l) = i;
end

Is there anything I can do to speed this up? Can the code be vectorized?

Answer 1

If I understand correctly, you want to know how many items fell in each bucket. Use:

n = hist(Y,nbins)

Though I am not sure that it will help in the speedup. It is just cleaner this way.

Edit : Following the comment:

You can use the second output parameter of histc

[n,bin] = histc(...) also returns an index matrix bin. If x is a vector, n(k) = >sum(bin==k). bin is zero for out of range values. If x is an M-by-N matrix, then

Answer 2

I think you shoud use histc

[~,Y] = histc(X,q)

As you can see in matlab's doc:

Description

n = histc(x,edges) counts the number of values in vector x that fall between the elements in the edges vector (which must contain monotonically nondecreasing values). n is a length(edges) vector containing these counts. No elements of x can be complex.

Answer 3

How About this

function [Y q] = levels(X,nLevels)

p = linspace(0, 1.0, nLevels+1);
q = quantile(X,p); 
Y = zeros(size(X));
for i = 1:numel(q)-1    
    Y = Y+ X>=q(i);
end

This results in the following:

>>X = [3 1 4 6 7 2];
>>[Y, q] = levels(X,2)

Y =

     1  1  2  2  2  1

q =

     1  3.5  7

You could also modify the logic line to ensure values are less than the start of the next bin. However, I don't think it is necessary.

Answer 4

I made a couple of refinements (including one inspired by Aero Engy in another answer) that have resulted in some improvements. To test them out, I created a random matrix of a million rows and 100 columns to run the improved functions on:

>> x = randn(1000000,100);

First, I ran my unmodified code, with the following results:

Note that of the 40 seconds, around 14 of them are spent computing the quantiles - I can't expect to improve this part of the routine (I assume that Mathworks have already optimized it, though I guess that to assume makes an...)

Next, I modified the routine to the following, which should be faster and has the advantage of being fewer lines as well!

function [Y q] = levels(X,nLevels)

p = linspace(0, 1.0, nLevels+1);
q = quantile(X,p);
if isvector(q), q = transpose(q); end

Y = ones(size(X));

for i = 2:nLevels
    Y = Y + bsxfun(@ge,X,q(i,:));
end

The profiling results with this code are:

So it is 15 seconds faster, which represents a 150% speedup of the portion of code that is mine, rather than MathWorks.

Finally, following a suggestion of Andrey (again in another answer) I modified the code to use the second output of the histc function, which assigns entries to bins. It doesn't treat the columns independently, so I had to loop over the columns manually, but it seems to be performing really well. Here's the code:

function [Y q] = levels(X,nLevels)

p = linspace(0,1,nLevels+1);

q = quantile(X,p);
if isvector(q), q = transpose(q); end
q(end,:) = 2 * q(end,:);

Y = zeros(size(X));

for k = 1:size(X,2)
    [junk Y(:,k)] = histc(X(:,k),q(:,k));
end

And the profiling results:

We now spend only 4.3 seconds in codes outside the quantile function, which is around a 500% speedup over what I wrote originally. I've spent a bit of time writing this answer because I think it's turned into a nice example of how you can use the MATLAB profiler and StackExchange in combination to get much better performance from your code.

I'm happy with this result, although of course I'll continue to be pleased to hear other answers. At this stage the main performance increase will come from increasing the performance of the part of the code that currently calls quantile. I can't see how to do this immediately, but maybe someone else here can. Thanks again!

Answer 5

You can sort the columns and divide+round the inverse indexes:

function Y = levels(X,nLevels)
% "Assign each of the elements of X to an integer-valued level"
[S,IX]=sort(X);
[grid1,grid2]=ndgrid(1:size(IX,1),1:size(IX,2));
invIX=zeros(size(X));
invIX(sub2ind(size(X),IX(:),grid2(:)))=grid1;
Y=ceil(invIX/size(X,1)*nLevels);

Or you can use tiedrank:

function Y = levels(X,nLevels)
% "Assign each of the elements of X to an integer-valued level"
R=tiedrank(X);
Y=ceil(R/size(X,1)*nLevels);

Surprisingly, both these solutions are slightly slower than the quantile+histc solution.