Compacting a digraph in Graphviz using Dot Language

Question

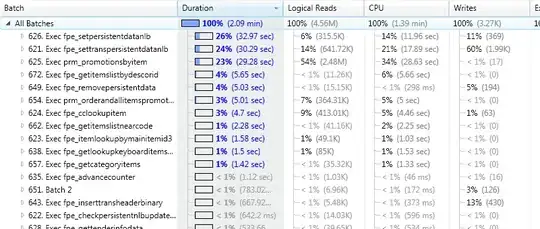
I'm trying to achieve a visualization of a specific graph (a Cayley graph of a symmetric permutation group) as the one done here but using Graphviz 2.28 with Dot.

_{(source: euclideanspace.com)}

digraph cayley {
    i -> x [color=red];
    i -> y [color=blue];
    x -> xx [color=red];
    x -> xy [color=blue];
    y -> yx [color=red];
    y -> yy [color=blue];
    xx -> xxx [color=red];
    xx -> xxy [color=blue];
    xy -> xyx [color=red];
    xy -> xyy [color=blue];
    yx -> yxx [color=red];
    yx -> xyx [color=blue];
    yy -> yyx [color=red];
    yy -> yyy [color=blue];
    xxx -> i [color=red];
    xxx -> xxxy [color=blue];
    xxy -> xxyx [color=red];
    xxy -> xxyy [color=blue];
    xyx -> xyxx [color=red];
    xyx -> xxyx [color=blue];
    xyy -> yy [color=red];
    xyy -> xyyy [color=blue];
    yxx -> yxxx [color=red];
    yxx -> xx [color=blue];
    yyx -> xxyy [color=red];
    yyx -> xyxx [color=blue];
    yyy -> yyyx [color=red];
    yyy -> i [color=blue];
    xxxy -> xxxyx [color=red];
    xxxy -> yyx [color=blue];
    xxyx -> yyy [color=red];
    xxyx -> xxxyx [color=blue];
    xxyy -> xyy [color=red];
    xxyy -> yxx [color=blue];
    xyxx -> xyxxx [color=red];
    xyxx -> xxx [color=blue];
    xyyy -> xyyyx [color=red];
    xyyy -> x [color=blue];
    yxxx -> y [color=red];
    yxxx -> xyyyx [color=blue];
    yyyx -> xxy [color=red];
    yyyx -> xyxxx [color=blue];
    xxxyx -> xyyy [color=red];
    xxxyx -> yx [color=blue];
    xyxxx -> xy [color=red];
    xyxxx -> yxxx [color=blue];
    xyyyx -> xxxy [color=red];
    xyyyx -> yyyx [color=blue];
}

My Dot generates the following layout: 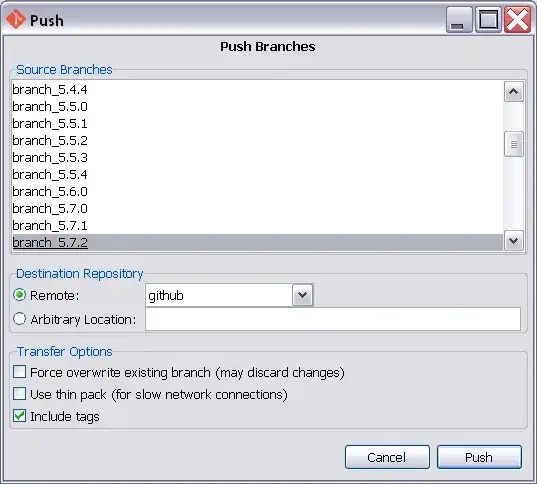cayley which is a pretty huge graph compared with the previous one. Is there any attribute that can compact the graph as close as possible to the first one ?

... and I've tried [the solution](http://stackoverflow.com/questions/3428448/reducing-graph-size-in-graphviz) from @doug and it doesn't work in this case. — mihaipopescu, Dec 22 '11 at 23:21

allenchen · Accepted Answer · 2011-12-23T01:15:46.113

I modified the codes such as graph, node and edge default attributes to make the layout as compacted as possible. Maybe there is a more perfect approach. By the way, the node i is located at the left but not right.

digraph cayley {
    graph[rankdir=LR, center=true, margin=0.2, nodesep=0.1, ranksep=0.3]
    node[shape=circle, fontname="Courier-Bold", fontsize=10, width=0.4, height=0.4, fixedsize=true]
    edge[arrowsize=0.6, arrowhead=vee]
    i -> x [color=red];
    i -> y [color=blue];
    x -> xx [color=red];
    x -> xy [color=blue];
    y -> yx [color=red];
    y -> yy [color=blue];
    xx -> xxx [color=red];
    xx -> xxy [color=blue];
    xy -> xyx [color=red];
    xy -> xyy [color=blue];
    yx -> yxx [color=red];
    yx -> xyx [color=blue];
    yy -> yyx [color=red];
    yy -> yyy [color=blue];
    xxx -> i [color=red];
    xxx -> xxxy [color=blue];
    xxy -> xxyx [color=red];
    xxy -> xxyy [color=blue];
    xyx -> xyxx [color=red];
    xyx -> xxyx [color=blue];
    xyy -> yy [color=red];
    xyy -> xyyy [color=blue];
    yxx -> yxxx [color=red];
    yxx -> xx [color=blue];
    yyx -> xxyy [color=red];
    yyx -> xyxx [color=blue];
    yyy -> yyyx [color=red];
    yyy -> i [color=blue];
    xxxy -> xxxyx [color=red];
    xxxy -> yyx [color=blue];
    xxyx -> yyy [color=red];
    xxyx -> xxxyx [color=blue];
    xxyy -> xyy [color=red];
    xxyy -> yxx [color=blue];
    xyxx -> xyxxx [color=red];
    xyxx -> xxx [color=blue];
    xyyy -> xyyyx [color=red];
    xyyy -> x [color=blue];
    yxxx -> y [color=red];
    yxxx -> xyyyx [color=blue];
    yyyx -> xxy [color=red];
    yyyx -> xyxxx [color=blue];
    xxxyx -> xyyy [color=red];
    xxxyx -> yx [color=blue];
    xyxxx -> xy [color=red];
    xyxxx -> yxxx [color=blue];
    xyyyx -> xxxy [color=red];
    xyyyx -> yyyx [color=blue];
    { rank=same; x; y }
    { rank=same; xx; xy; yx; yy }
    { rank=same; xxx; xxy; xyx; xyy; yxx; yyx; yyy }
    { rank=same; xxxy; xxyx; xxyy; xyxx; xyyy; yxxx; yyyx }
    { rank=same; xxxyx; xyxxx; xyyyx }
}

The image is shown as following.

enter image description here

Compacting a digraph in Graphviz using Dot Language

1 Answers1

Linked