A recent post on the Wolfram Blog offered the following function to format derivatives in a more traditional way.
pdConv[f_] :=
TraditionalForm[
f /. Derivative[inds__][g_][vars__] :>
Apply[Defer[D[g[vars], ##]] &,
Transpose[{{vars}, {inds}}] /. {{var_, 0} :>
Sequence[], {var_, 1} :> {var}}]
]
An example use, Dt[d[x, a]] // pdConv gives:
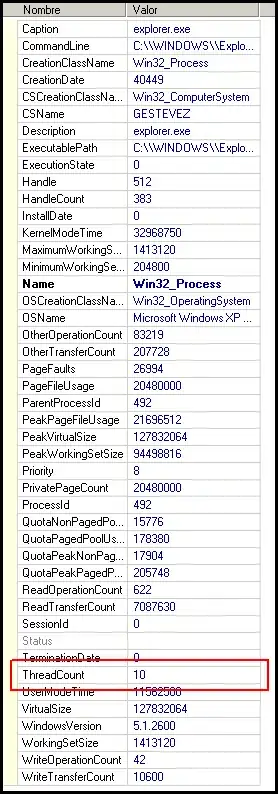
Without breaking the general capabilities of pdConv, can someone alter it to maintain the given order of variables, producing the output shown below? (of course this is purely for asthetic reasons, making derivations easier for a human to follow)
I suspect this will be nontrivial to implement---unless someone knows of a magical Global option that can be temporarily overridden within a Block.
For what it's worth, these SO questions may be related:
