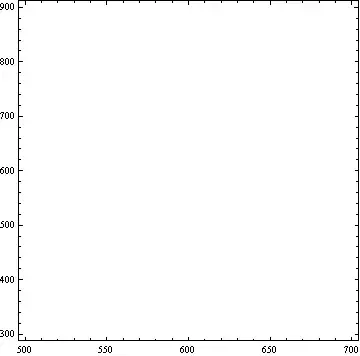
When exporting rather complicated plots (especially ListDensityPlot) as a PDF or EPS (for publication, for example), the resulting file size can be quite large. For example:
data = Flatten[Table[{f0, f, Exp[-(f - f0)^2/25^2]}, {f0, 500, 700, 5}, {f, 300,
900}], 1];
plot=ListDensityPlot[data,PlotRange->{Automatic,Automatic,{0,1}},InterpolationOrder->0]
This example data set is on the order of the size I typically work with. When I export using Export["C:\\test.pdf", plot], it generates a PDF file 23.9MB in size. If I instead try Export["C:\\test1.pdf", Rasterize[plot]] it is far smaller, but the integrity and rescalability of the image naturally suffers.
This is complicated further if my actual figure is a combined plot, such as (Edit: f goes to 900)
plot2 = Show[plot, Plot[x, {x, 500, 900}, PlotStyle -> Thick]]
(or with some usage of Epilog) where I'd love to have the background ListDensityPlot be rasterized, but keep the other markup and plots in ``vector'' form. Or at the very least, the frame labels be non-rasterized.
Is there any way to do this?
Or, to accomplish the same goal via some other clever method?
Update
I've checked out the related question, but that's gotta be way more complicated than it needs to be (essentially exporting then importing). I've been able to utilize some of the tricks in that question to extract the plot separately from the axes:
axes = Graphics[{}, Options[plot2]]
plots = Graphics[plot2[[1]]]
But, the plots term loses the AspectRatio and PlotRange, etc. plots can be hit with a Rasterize, but it needs dimensional fixing.
And then, how to combine them together?