I want to use matplotlib to make a 3d plot given a z function

Question

I have a z function that accepts x and y parameters and returns a z output. I want to plot this in 3d and set the scales. How can I do this easily? I've spent way too much time looking through the documentation and not once do I see a way to do this.

Answer 1

The plotting style depends on your data: are you trying to plot a 3D curve (line), a surface, or a scatter of points?

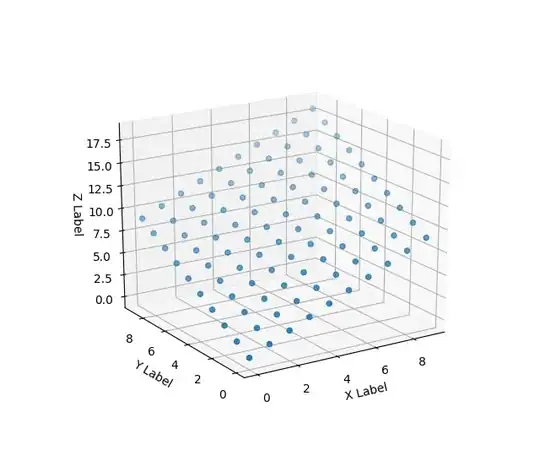
In the first example below I've just used a simple grid of evenly spaced points in the x-y plane for the domain. Generally, you first create a domain of xs and ys, and then calculate the zs from that.

This code should give you a working example to start playing with:

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import random

def fun(x, y):
    return x + y

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
n = 10
xs = [i for i in range(n) for _ in range(n)]
ys = list(range(n)) * n
zs = [fun(x, y) for x,y in zip(xs,ys)]

ax.scatter(xs, ys, zs)

ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')

plt.show()

---

For surfaces it's a bit different, you pass in a grid for the domain in 2d arrays. Here's a smooth surface example:

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import random

def fun(x, y):
    return x**2 + y

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
x = y = np.arange(-3.0, 3.0, 0.05)
X, Y = np.meshgrid(x, y)
zs = np.array([fun(x,y) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)

ax.plot_surface(X, Y, Z)

ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')

plt.show()

For many more examples, check out the mplot3d tutorial in the docs.