What's the best method to compare original trajectory with two compressed trajectory

Question

Suppose to have a GPS trajectory - i.e.: a series of spatio-temporal coords, every coord is a (x,y,t) information, where x is longitude, y is latitude and t is the time stamp. Suppose each trajectory identified by 1000 (x,y) points, a compressed trajectory is trajectory with fewer points than the original, for instance 300 points. A compression algorithm (Douglas-Peucker, Bellman, etc) decide what points will be in compressed trajectory and what point will be discarded.

Each algorithm make his own choice. Better algorithms choice the points not only by spatial characteristics (x, y) but using spatio-temporal characteristics (x,y,t).

Now I need a way to compare two compressed trajectories against the original to understand what compression algorithm better reduce a spatio-temporal (temporal component is really important) trajectory.

I've thinked of DTW algorithm to check trajectory similarity, but this probably don't care about temporal component. What algorithm can I use to make this control?

Answer 1

What is the best compression algorithm depends to a large extent on what you are trying to achieve with it, and is dependent on other external variables. Typically, were going to identify and remove spikes, and then remove redundant data. For example;

Known minimum and maximum velocity, acceleration, and ability to tuen will let you remove spikes. If we look at the join distance between a pair of points divided by the time where

velocity = sqrt((xb - xa)^2 + (yb - ya))/(tb-ta)

we can eliminate points where the distance couldn't be travelled in the elapsed time given the speed constraint. We can do the same with acceleration constraints, and change in direction constraints for a given velocity. These constraints change whether the GPS receiver is static, hand held, in a car, in an aeroplane etc...

We can remove redundant points using a moving window looking at three points, where if the an interpolated (x,y,t) for middle point can be compared with an observed point, and the observed point removed if it lies within a specified distance + time tolerance of the interpolated point. We can also curve fit the data and consider the distance to the curve rather than using a moving 3 point window.

The compression may also have differing goals based on the constraints given, e.g. to simply reduce the data size by removing redundant observations and spikes, or to smooth the data as well.

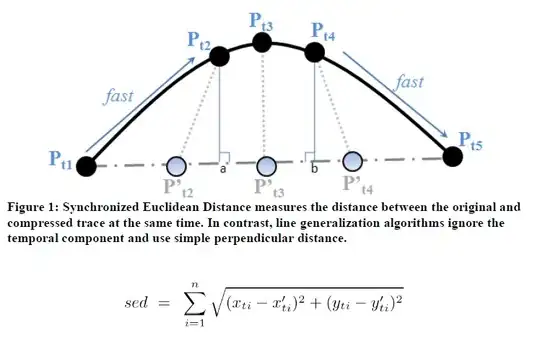
For the former, after checking for spikes based on defined constraints, we simply check the 3d distance of each point to the polyline connecting the compressed points. This is achieved by finding the pair of points before and after the point that has been removed, interpolating a position on the line connecting those points based on the observed time, and comparing the interpolated position with the observed position. The amount of points removed will increase as we allow this distance tolerance to increase.

For the latter we also have to consider how well the smoothed result models the data, the weights imposed by the constraints, and the design shape / curve parameters.

Hope this makes some sense.

Answer 2

Maybe you could use mean square distance between trajectories over time.
Probably, simply looking at distance at time 1s,2s,... will be enough, but you can also do it more precise between time stamps integrating, (x1(t)-x2(t))^2 + (y1(t)-y2(t))^2. Note that between 2 time stamps both trajectories will be straight line.

Answer 3

I've found what I need to compute spatio-temporal error. As written in paper "Compression and Mining of GPS Trace Data: New Techniques and Applications" by Lawson, Ravi & Hwang:

Synchronized Euclidean distance (sed) measures the distance between two points at identical time stamps. In Figure 1, five time steps (t1 through t5) are shown. The simplified line (which can be thought of as the compressed representation of the trace) is comprised of only two points (P't1 and P't5); thereby, it does not include points P't2, P't3 and P't4. To quantify the error introduced by these missing points, distance is measured at the identical time steps. Since three points were removed between P't1 and P't5, the line is divided into four equal sized line segments using the three points P't2, P't3 and P't4 for the purposes of measuring the error. The total error is measured as the sum of the distance between all points at the synchronized time instants, as shown below. (In the following expression, n represents the total number of points considered.)