I saw this in some paper and someone argued that there can be at most log(n) times rotation when we delete a node of an AVL tree. I believe we can achieve this by generating an AVL tree as lopsided as possible. The problem is how to do this. This will help me a lot about researching the removal rotation thing. Thanks very much!
Asked
Active
Viewed 1,700 times
5
-
See also: http://stackoverflow.com/questions/19622572/how-to-generate-maximally-unbalanced-avl-trees – Walter Tross Nov 06 '13 at 12:37
1 Answers
9
If you want to make a maximally lopsided AVL tree, you are looking for a Fibonacci tree, which is defined inductively as follows:
- A Fibonacci tree of order 0 is empty.
- A Fibonacci tree of order 1 is a single node.
- A Fibonacci tree of order n + 2 is a node whose left child is a Fibonacci tree of order n and whose right child is a Fibonacci tree of order n + 1.
For example, here's a Fibonacci tree of order 5:
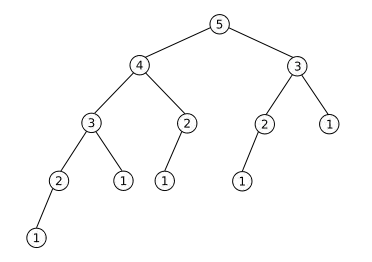
The Fibonacci trees represent the maximum amount of skew that an AVL tree can have, since if the balance factor were any more lopsided the balance factor of each node would exceed the limits placed by AVL trees.
You can use this definition to very easily generate maximally lopsided AVL trees:
function FibonacciTree(int order) {
if order = 0, return the empty tree.
if order = 1, create a single node and return it.
otherwise:
let left = FibonacciTree(order - 2)
let right = FibonacciTree(order - 1)
return a tree whose left child is "left" and whose right child is "right."
Hope this helps!
templatetypedef
- 362,284
- 104
- 897
- 1,065
-
1
-
(Note in particular that every non-leaf has balance "factor" different from 0.) – Erik P. Jan 25 '12 at 18:13