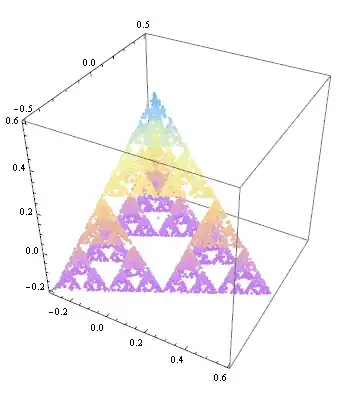
I have written code which draws the Sierpinski fractal. It is really slow since it uses recursion. Do any of you know how I could write the same code without recursion in order for it to be quicker? Here is my code:
midpoint[p1_, p2_] := Mean[{p1, p2}]
trianglesurface[A_, B_, C_] := Graphics[Polygon[{A, B, C}]]
sierpinski[A_, B_, C_, 0] := trianglesurface[A, B, C]
sierpinski[A_, B_, C_, n_Integer] :=
Show[
sierpinski[A, midpoint[A, B], midpoint[C, A], n - 1],
sierpinski[B, midpoint[A, B], midpoint[B, C], n - 1],
sierpinski[C, midpoint[C, A], midpoint[C, B], n - 1]
]
edit:
I have written it with the Chaos Game approach in case someone is interested. Thank you for your great answers! Here is the code:
random[A_, B_, C_] := Module[{a, result},
a = RandomInteger[2];
Which[a == 0, result = A,
a == 1, result = B,
a == 2, result = C]]
Chaos[A_List, B_List, C_List, S_List, n_Integer] :=
Module[{list},
list = NestList[Mean[{random[A, B, C], #}] &,
Mean[{random[A, B, C], S}], n];
ListPlot[list, Axes -> False, PlotStyle -> PointSize[0.001]]]