23

I am at learning stage of cyclomatic complexity(CC). For practise, I am calculating cyclomatic complexity of 2 examples and want to confirm if my answers are correct or not...

Referring to wikipedia, CC is given by M = E − N + 2P where:

  • E = the number of edges of the graph
  • N = the number of nodes of the graph
  • P = the number of connected components

Please help.

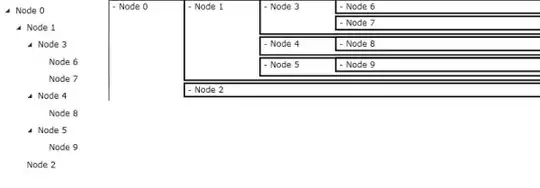
Example 1

Here, E = 8, N = 9 and P = 1. Hence M = 8 - 9 + (2x1) = 1.

Example 2:

Example 2

Here E = 11, N = 10 and P = 1. Hence M = 10 - 11 + (2x1) = 1.

Hence for both the examples CC is 1. Please let me know if my calculation is correct or not.

cdeszaq
  • 30,869
  • 25
  • 117
  • 173
tech_human
  • 6,592
  • 16
  • 65
  • 107
  • 5
    I'm voting to close this question as off-topic because it is workflow-based math. This belongs on Software Engineering, not Stack Overflow. – TylerH Jan 25 '17 at 17:32

4 Answers4

23

You need to take more care to correctly insert the values into the formula.

In example 1, you say

Here, E = 8, N = 9 and P = 1

But actually, it's the other way round: 9 edges (=E), 8 nodes (=N), so you get a CC of 3.

In example 2, you have the values right: E=11, N=10, P=1. But you insert them in the wrong order in the formula; it actually should be 11 - 10 + (2x1) = 3.

Shortcut: If you have a picture of your graph, you can very easily determine the cyclomatic complexity. Just count the number of regions the background is divided into by the edges. In your first example, you have 2 inner regions (bordered by the edges) and one surrounding region, giving a CC of 3. Same goes with the second example. (This method requires that edges are not crossing each other, obviously.)

flyx
  • 35,506
  • 7
  • 89
  • 126
  • 1
    +1, didn't know that background division method :) – Kos Feb 01 '12 at 15:19
  • Ohh yes... I have noted wrong values by mistake... Thanks for pointing in out and helping me with the answers. Also +1, for the shortcut method... I didn't knew that. :) – tech_human Feb 01 '12 at 15:23
  • Another +1 for the **shortcut** - works like a charm. –  Jul 26 '16 at 10:44
  • Why in the first example is correct to count the point where two arrows meet as a node, but in the second example is not correct to do it? – XtianGIS Sep 27 '16 at 19:52
  • @XtianGIS this is merely a cosmetic difference, you can do either. It will not change the result of the calculation. – flyx Sep 28 '16 at 06:40
8

Also if this helps, it the number of conditional (If, while, for) statements +1. So in the above example, there are 2 conditional statements . so 2+1=3. Cyclomatic complexity in this case is 3

Stephan
  • 41,764
  • 65
  • 238
  • 329
Neethi
  • 81
  • 1
  • 1
  • 1
    Do you have a reference for this heuristic? – Apalala Sep 13 '16 at 00:20
  • 1
    @Apalala This is valid for any control flow graph with just *one entry* and just *one exit* point. It was shown by Thomas J. MacCabe. Refer [here](https://dx.doi.org/10.1109%2Ftse.1976.233837) – Quirk May 03 '17 at 19:13
1

Just count the number of closed region and add 1 to it.

In your example above, number of closed region = 2, so the CC = 2+1 = 3

Oli
  • 1,132
  • 1
  • 12
  • 26
Nik cool
  • 11
  • 1
0

P = the number of connected components

IN OTHER WORDS

P = the number of nodes that have exit points

Source

Raviteja
  • 3,399
  • 23
  • 42
  • 69
Adrián Sabo
  • 9
  • 1