Is there a Java library with 3D spline functions?

Question

In particular, I need a way to represent a curve/spline that passes through a set of known 3D points, and a way of finding other points on the curve/spline, by subdivision/interpolation.

For example, if I have a set of points P0 to PN, I want to find 100 points between P0 and P1 that are on a spline that passes through P0 and P1.

I see that Java3D's KBRotPosScaleSplinePathInterpolator performs such a calculation, but it is tied to that API's scenegraph model and I do not see how to return the values I need.

Answer 1

You're looking for something like a Catmull Rom spline. The reality is that the math just isn't all that hard to deal with (some vector-matrix multiplications). My recommendation is that you just implement the spline that you really need in code.

Quoting from that article:

The points that define a spline are known as "Control Points". One of the features of the Catmull-Rom spline is that the specified curve will pass through all of the control points - this is not true of all types of splines.

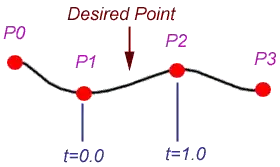
To calculate a point on the curve, two points on either side of the desired point are required, as shown on the left. The point is specified by a value t that signifies the portion of the distance between the two nearest control points.

You should be aware, though, that the Catmull-Rom spline can lead to little loops at the control points if they are too close together when they need to take a tight turn.

Looking at the image above, imagine that p1 and p3 were right next to each other, below p2 (basically compressing the right hand side of the picture). It's likely that a Catmull-Rom spline would come down from p0, pass through p1 as it does now, go up the right side of p2 and pass through it from right to left, coming down the left hand side and passing left to right through p3.

This is a consequence of the construction of the spline.

It's sort of like working with fairly stiff flexible pipe (like I have under my sink). In order to get a longish piece to connect to points that are close together, I have to add a loop.

Answer 2

For anyone struggling with the maths behind curves, you may find this useful, in particular the images below. The idea is simple:

Let t loop from 0.0 to 1.0.

For each pair of points in the grey set, calculate a point a fraction of the way in between them (using t). These points are shown in green.

For each pair of points in the green set, calculate a point a fraction of the way in between them (using t). This point is shown in black.

For the different values of t, the black point will be a different line along a curve.

The second image shows the same process repeated with an extra point and an extra level of interpolation.

I found this much easier to understand, implement, and extend to 3 dimensions, than any other option I found.

approximating a curve using linear interpolation http://bimixual.org/AnimationLibrary/Bezier_2_big.gif approximating a curve using linear interpolation http://bimixual.org/AnimationLibrary/Bezier_3_big.gif

Answer 3

I have a good understanding of linear interpolation, but I found it difficult to grasp the complexity of the maths of splines. That is why I was looking for a library of some sort that would provide an abstraction to hide the difficult maths. The following function turned out to be sufficient for my needs. This is based on an equation found at http://www.mvps.org/directx/articles/catmull/ , but luckily you don't need to understand how it works. Just remember that unlike linear interpolation where you only need two points to start with, Catmull-Rom spline interpolation uses an extra point at either end. So if you want a spline that passes through 10 points, you need 12.

This function demonstrates Catmull-Rom spline interpolation in one dimension. (For 2 or 3 dimensions simply repeat using Y or Z values.) This function will give us a point on the spline between p1 and p2, where t is the proportion of the distance between the two.

public class SplineTest {

    // Catmull-Rom spline interpolation function
    public static double q(double t, double p0, double p1, double p2, double p3) {

        return 0.5 * ((2 * p1) + (-p0 + p2) * t
                + (2 * p0 - 5 * p1 + 4 * p2 - p3) * (t * t) + (-p0 + 3 * p1 - 3
                * p2 + p3)
                * (t * t * t));
    }

    public static void main(String[] args) {
        double t = 0.0;
        while (t <= 1.0) {
            System.out.println(q(t, 5, 10, 20, 10));
            t += 0.1;
        }
    }
}

This program outputs:

10.0
10.887500000000001
12.0
13.2625
14.6
15.9375
17.2
18.3125
19.2
19.7875
20.000000000000004

Answer 4

http://www.ee.ucl.ac.uk/~mflanaga/java/Interpolation.html

Answer 5

There's no built-in library that I'm aware of. Source

Answer 6

I have not tried it yet, but will most probably try it soon for generating 3d surface mesh out of random point inputs: toxiclib as a Spline3d tool

http://code.google.com/p/toxiclibs

Answer 7

I have just tried libGDX, Apache Licence http://github.com/libgtx/libgtx

It contains a BSpline class and is easy to use.

https://github.com/Graphics3D/ect/blob/master/src/main/java/courbes_bsplines/TestGDXBSpline.java