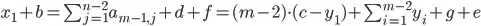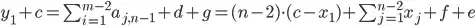What is an efficient way to generate a random contingency table? A contingency table is defined as a rectangular matrix such that the sum of each row is fixed, and the sum of each column is fixed, but the individual elements may be anything as long as the sum of each row and column is correct.
Note that it's very easy to generate random contingency tables, but I'm looking for something more efficient than the naive algorithm.
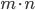 variables with
variables with 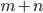 linear constraints leads to the expectation that the solution space has
linear constraints leads to the expectation that the solution space has 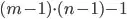 degrees of freedom.
degrees of freedom.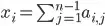 and
and 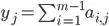 .
.